Learning Resources
Lesson
If events A and B are independent, then A does not change the probability of B .For example, if you roll a die and flip a coin, the probability of rolling a specific number on the die is in no way connected to the probability of heads or tails on the coin. However, some events influence others. For example, if you select a card from a regular 52-card deck and do not replace it, then the selection of the second card is dependent on the first since there are now only 52 cards left in the deck for the total possible outcomes. The investigation explores this situation.
In Step A, you should name the events; let event A be "removing a heart for the first card" and B is "removing a heart for the second card". When the first card is replaced in the deck, then the second choice in not influenced by the first and the events are independent. Therefore, the overall probabilities can be calculated as a product of the two probabilities 
or represented as follows:
For Step B, these events are dependent because the selection of the second card does affect the probability of a heart as the second card. For the first draw, all of the hearts are present for the 52 card deck; however for the second draw there will be one less heart and one less card in the deck. The probability of drawing two hearts is still calculated as above using the formula.
Example 1
Two cards are removed from a well-shuffled deck. What is the probability that both will be face cards?
Solution
Let A be "the first card is a face card" and let B be "the second card is a face card".
since there are 12 face cards in a deck of 52
since there are 11 face cards remaining out of the 51 cards left in the deck after event A .
Therefore, 
is
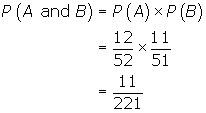
Example 2
You are dealt a hand of 5 cards from a regular deck of 52 playing cards. Four of them are hearts and the other a spade. You discard the spade and ask for another card. What is the probability the new card you receive is a heart? Is this an example of dependent or independent events?
Solution
Since you have 5 cards, there are only 47 remaining from which to choose. The "total number of possible outcomes" (cards left) is 47. Also, since you have 4 hearts there are only 9 left in the deck. The "number of ways of the desired event occurring" (red cards left) is 9. The probability the new card is a heart is:
Dependent and independent does not apply since there is only one event involved in this example, viz. "receiving a heart". You just have to be careful how you count the total and desired outcomes.
Activity
Investigation Questions p 311. Complete 13, 14 and 15
Check Your Understanding p.311 - 312. Complete 16, 17, 18, 19 and 20
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
- One fair coin is flipped 2 times. Event A is "a head occurs on the first flip" and event B is "a head occurs on the second flip". Are A and B dependent or independent? Explain.
- An urn contains 4 balls numbered 1, 2, 3, 4 respectively. Two balls are drawn without replacement. Event C is "the first ball drawn has a 1 on it" and event D is "the second ball drawn has a 1 on it". Are C and D dependent or independent? Explain.
Click here for suggested solution.