
Learning Resources
Lesson
In the first lesson in this unit we learned the formula for calculating theoretical probability. It stated that the probability a given event X will occur, denoted as P(X), is calculated as follows:
![]()
To use this formula, we have to be able to count the numbers in both the numerator and denominator. As we have said before, theoretical probability involves counting. In the examples discussed so far, the counting has been fairly easy. However, there are situations that present some difficulties when we try to count them.
The rest of this unit is devoted to devising methods of counting that will assist us in calculating theoretical probability. The first of these methods is referred to as the Fundamental Counting Principal. To help understand it consider the following example
Example 1
If a coin is tossed and a six sided die is rolled, what is the probability we will get a head on the coin and a 5 on the die?
Solution
We have to count the number of ways the event can happen and compare it to the total number of possible outcomes. One way of doing this is to construct a tree diagram, which those of you who have done Math 2204 should remember how to do. Use the interactive window below to generate the tree diagram for this problem. You can generate it in a step by step fashion or view the completed tree.
From the above "tree" you should be able to see that the total number of possible outcomes for this situation is 12 and the number of ways the desired event could occur is 1. Thus we can say:
![]()
Note that there were two possibilities for the coin (head or tail) and six possibilities for the die (1, 2, 3, 4, 5, 6). The aim of this investigation is to see how to use these numbers to calculate the total number of possible outcomes without having to draw a tree diagram.
Having considered the above example complete Investigation 3 on page 307 in your text.
In Step A there are three categories of choices; you may start your diagram with any one of the categories, however, it is a good idea to start with the category with the least number of choices. You can also break the diagram into two parts to accommodate the size of your paper. For Step B, you should notice that multiplication can be used to find the total number of choices rather than counting every individual choice.
The Fundamental Counting Principle states that if an event consists of several parts or stages, then the size of the sample space is equal to the product of the numbers of possibilities that exist for each part or stage.
Example 2
A television manufacturer has 8 different sizes to choose from. Each size can be purchased with or without the option of a built in VCR, a built in DVD player, or both. The TVs come in black, ivory and metal casings. How many different "models" do they produce?
Solution
8 (sizes) X 4 (options) X 3 (casings) = 96 "models"
The probability formula
![]()
in Section 5.1 is useful when you can count the number of values for both the numerator and denominator. Focus B shows how the fundamental counting principle can be used to determine the value of the denominator (the total number of possible outcomes) and the value of the numerator (the number of favourable outcomes). Study the example given in your text. A further example is given below.
Example 3
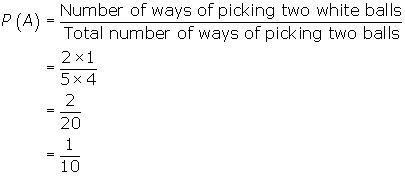
Three red balls and two white balls are place in a box. Suppose two balls are removed at random. What is the probability that the two balls will be white?
Solution
The probability of drawing the two white balls is
![]()
By the fundamental counting principle, you can pick two items by 2 choices for the first and 1 choice for the second which gives ![]() , which is number of ways of picking two white balls.
, which is number of ways of picking two white balls.
There are a total of 5 balls in the box. There are 5 ways to choose the first ball and 4 ways to choose the second - by the fundamental counting principle, the total number of ways of pricking two balls is ![]() .
.
If event A represents picking two white balls, the probability is
Activity
Investigation Questions p.308 . Complete 1 and 2
Think About p.307, p.308 and p.309
Check Your Understanding p.308 - 309. Complete 3 to 9 inclusive
Check Your Understanding p.310. Complete 10, 11 and 12
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
For lunch, a restaurant offers a full meal deal which has the following options: a salad or bowl of soup; a sandwich of turkey, chicken, roast beef, or salami; a drink of coffee, tea, or soft drink; a dessert of apple pie or fruit cup. Just as you finish your meal you notice two friends in a corner booth. When you spoke to them you found out they each had a different option for lunch. What is the probability that you had exactly the same option as one of them?
Click here for a suggested solution.