
Learning Resources
Lesson
As an introduction to this topic consider the following scenario.
Dick and Jane are each given a large opaque bag containing marbles of different colours. They are asked the same question: "If one marble is selected from the bag, what is the probability that it is red?" They decide to proceed in different ways to determine this probability.
Dick dumps all the marbles out of the bag, counts the total number of marbles in the bag and then counts the number of of these which are red ones. He concludes that the probability of picking a red marble is as follows:
![]()
Jane decides on a different approach. She selects one marble from the bag, records its colour, and replaces it in the bag. She then shakes the bag to redistribute the marbles and repeats the process. She does this 50 times. She concludes that the probability of picking a red marble is as follows:
![]()
Who is correct? Are they both correct? Will their two answers ever be the same? Which method would you use if there were 100 marbles in the bag? 5000 marbles in the bag?
In the preceding example, neither Dick nor Jane were wrong. They calculated different versions of the probability. Probability is defined as a ratio of the number of ways of obtaining a particular outcome, such as picking a red marble, to the total number of possible outcomes.
Dick's calculation gave the theoretical probability. Theoretical probability is the ratio that you would expect to occur. Theoretical probability of success involves finding the ratio of the number of ways that you can achieve success (e.g. how many red marbles were in the bag) compared to the total number of possible outcomes (total number of marbles in the bag). The formula for finding it is generally written as:
![]()
Jane's calculation gave the experimental probability. Experimental probability is an estimate of the probability of a successful event occurring (picking a red marble). It is calculated by taking the ratio of the number of successful trials compared to the total number of trials. It is found by conducting some sort of experiment in the real world, hence the name 'experimental'. The formula for it can be written as:
![]()
If you count the total possible number of ways of achieving a desired event and compare it to the total number of ways an event can occur, you have calculated the theoretical probability. Theoretical probability involves counting. Most of the work in this section deals with theoretical probability. In the first few examples in this lesson it is easy to count but we shall look at cases in later lessons where we will need special counting techniques to help us determine the number of outcomes.
Example 1
What is the theoretical probability of a 3 turning up on a roll of a single standard six faced die?
Solution
Here the counting is very easy. There are only 6 possible outcomes for the roll of a die, viz. 1, 2, 3, 4, 5, and 6. Of these, only one gives success of the desired event, viz. 3. Hence the probability of a 3 turning up is:![]()
The notation P(X) means the probability of event X occurring. In the above example X is 'a three turning up on a single roll'.
In the above example the question could also have been asked, "What is the probability of a 3 NOT turning up on a single roll?". That event is referred to as the complement of the event in the above example. The complement of an event X is the event NOT X. The notation used for the probability of the complement is P(X). There are 5 ways that 3 could not turn up (1, 2, 4, 5, and 6). Hence the probability of X is:![]()
You should note that P(X) can also be found by subtracting P(X) from 1. That is ![]()
Using this for the above example, "What is the probability of a 3 NOT turning up on a single roll?", we get: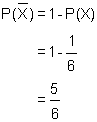
Which is the same result obtained by using our previous method to calculate the probability.
This also points out the fact that there is often more than one approach to take in solving a probability problem.
So far we have been discussing probability. Many people get probability confused with odds. Although they are related they are not the same. The odds of an event X occurring is the ratio of event occurring to the event NOT occurring:![]()
In our example on the previous page, the ODDS of rolling a 3 on a single toss is:![]()
In the previous examples, both probability and odds have been expressed as fractions. It is equally correct to express either as a decimal. Thus a probability of ½ or 0.5 mean the same thing.
Also odds are more often expressed in ratio rather than fraction notation, for example ½ is written 1:2; ¼ is written 1:4, etc. Thus the odds in the above example would be expressed as 1:5.
Activity
Focus Questions p.301. Complete 1 and 2
Think About p.300 and p.301
Check Your Understanding p.301 302. Complete 3 to 11 inclusive
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
After you do the assigned activities, continue on to the Test Yourself section below for a quick quiz on this lesson.
(Note: Some of the activities in this unit involve playing cards. The features of a standard deck of cards include
- there are 52 cards in the deck
- there are four suits: hearts, diamonds, clubs and spades. Two suits - diamonds and hearts - are red and two suits are black
- each suit has 13 cards
- the "one" is referred to as the "ace"
- Jacks, queens, and kings, which feature pictures of people, are referred to as "face cards"; all other cards are number consecutively 2 through 10.)
Test Yourself
In a class of 20 students, one is to be chosen to receive a free lunch at a local restaurant. Two students are not interested in going and the rest put their names on a slip of paper, place it in a bag, and have the teacher draw a name. If you are one of the students in the class interested in going:
- What is the probability your name will be picked?
- What is the probability your name will not be picked?
- Why is this an example of theoretical probability?
- What are the odds your name will be picked?
Click here for suggested solutions.