
Learning Resources
Lesson
A circle is constructed in a co-ordinate plane with points that have co-ordinates that are dependent on the central angle in standard position for that point. In situations where variables depend upon another variable, such as the central angle for the circle, it is called a parameter. The equations relating x and y to that variable are called parametric equations. In a parametric equation, the x and y variables are each written as a function of a third variable t, called the parameter. For the circle this third variable is q , the measure of the central angle in standard position.
In this investigation the circle will be examined as a parametric equation through the TI-83 calculator. The steps in the Procedure are simple instructions for entering the functions and exploring some of the properties.
Steps A through E are instructions for entering the parametric equations into your calculator. Step B is important since your window settings have to be correct to make your screen a square; if not your circles will not "look" right. The given settings will become your default for this lesson. If you require a larger window make sure that the settings are multiples of 4.7 for the x coordinate and 3.1 for the y coordinate.
When you enter the parametric equations in Step C, close off the open brackets. Although it is not always necessary, it is a good practice to get into.
Steps F through M lead you through changes in the Tstep in your window and how it affects the resulting graph. Complete these steps. Note the introduction of the term quadrantal angle.
As previous seen, the circle can be transformed on the plane. The Steps O to S carry you through this process.
Example 1
Graph ![]() and
and ![]() on the TI-83.
on the TI-83.
Solution
Click here to see a demonstration of how to enter this into your calculator.
You should enter this into your own calculator and make note of the centre of the circle and radius of the circle and how it relates to the equations.
Example 2
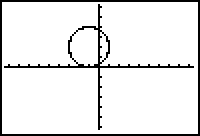
Graph a circle with radius 2 and centre (-1,2) using parametric equations.
Solution
The equations that represents the given information are
![]()
Entering these equations as above will give the following graph on the TI-83:
Activity
Investigation Questions p.276. Complete 16 to 22 inclusive
Check Your Understanding p.276 - 277. Complete 23, 24, 25, 26 and 27
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
- Write a parametric equation to graph a circle
- Graph this equation on your calculator
- Explain how to change the window settings on your graphing calculator so that an octagon is drawn
- Write a second parametric equation that will graph an ellipse, with the ten unit long major axis on the x axis and the eight unit long minor axis on the y axis.
- Modify your equation such that the ellipse lies completely in Quadrant 1.
Click here for suggested solutions.