Learning Resources
Lesson
If we are given an angle and asked to find its sine or cosine, we can simply enter the value directly into the calculator regardless of its value. Thus cos(352°) is found by simply entering 352 as the argument of the cos command button.
In this lesson we consider the opposite procedure. We will know the sine or cosine of the angle and we will be asked to determine the angle. To do this we have to use the inverse functions, denoted as sin-1 and cos-1 . (If you are not sure about the inverse trigonometric functions some extra notes are provided; Click here). Consider the following simple example:
Example 1
Find the measure of q in degrees if sin q = 0.2918.
Solution
The answer can found using the calculator. To see the procedure click here. The answer is 16.9°. That means that sin (16.9°) = 0.2918.
Let's look a little closer at the above solution and let's relate it to the unit circle. Look closely at the diagram below:
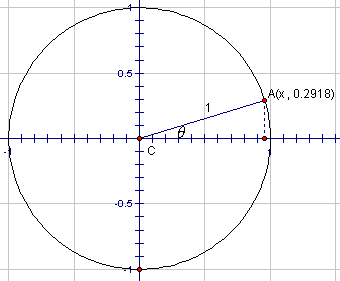
The angle we found of 16.9° is q and from the given information that is a correct solution. The y-co-ordinate is r sin q, but since r = 1 , the y-co-ordinate is simply sin q .
However, there is another angle whose sine (the y-coordinate of the point of intersection) is also 0.2918. It is in the second quadrant and is shown in the diagram below.
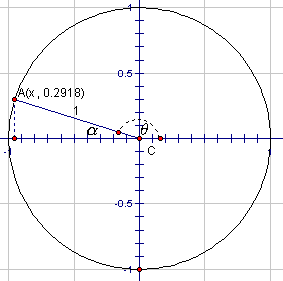
The 16.9° we found is actually the measure of a, the related angle. The measure of the angle q is 180° - 16.9° or 163.1°. Thus there are two angles, both less than 360° which satisfy the condition that its sine is 0.2918. When finding the inverse of the trigonometric ratios we have to take this into account. It is always best to first draw a diagram to consider the different possibilities.
Also note that there is no angle in the 3rd or 4th quadrant, because there the y-co-ordinate is negative and the sine of an angle is determined by the y-co-ordinate of the point.
We now want to explore examples where the circle is not the unit circle, i.e. its radius is not equal to 1.
Example 2
Find the measure of q to the nearest degree if, when it is put in standard position, the coordinates of the point where it intersects a circle of radius 6 units are ( 2.63 , - 5.39)
Solution
The first step is to sketch a diagram containing the given information. Note that since the x-co-ordinate of the point is positive and the y-co-ordinate is negative, the angle is in the fourth quadrant.
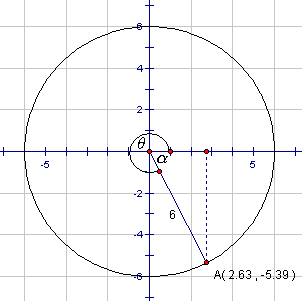
The next step is to find a, the related angle. We can use either the x or y co-ordinate. If we use the y-co-ordinate we can ignore the negative sign in our calculations, but we must remember which quadrant we are in since we only use a to determine the angle we wish to find, viz. q . Let's use the x-co-ordinate:
The related angle, a, is 64°. To find the desired angle, q , we simply subtract from 360°. Thus q = 360° - 64° = 296°.
Example 3
The terminal arm of an angle in standard position passes through (-4 , -3). Find the measure of the angle to the nearest degree.
Solution
The first step is to sketch a diagram containing the given information.
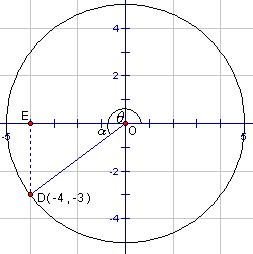
We wish to determine the value of the angle q . First, use trigonometry to determine the related angle a:
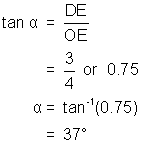
The related angle, a, is 37°. To find the desired angle, q , we simply add 180°. Thus q = 180° + 37° = 217°.
Up to now we have been using the calculator to find the value of the trigonometric ratios for the angles. However, it is possible to determine the exact value of many angles without using the calculator.
It is possible to find the exact values for the trigonometric ratios of certain angles. When you use a calculator you only find the approximate values for most angles. We will explore finding the exact values for angles of 30°, 45°, and 60°. Other angles, for which these are the related angles, are left for you to explore in the assigned work.
Let's first find the exact values of the trigonometric ratios for an angle of 45°. If we draw a right triangle and make one of its angles 45°, the other angle must also be 45° since the sum of the angles in a triangle is 180°. Since it has two equal angles, it is an isosceles right triangle and the legs are equal. This is shown in the diagram below.
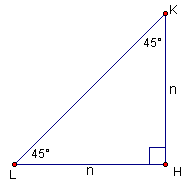
Since both sides are equal we can let n represent the length of each one. We now find an expression for the length of the hypotenuse using the Pythagorean theorem:
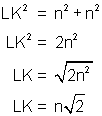
Using the diagram above and the measure just calculated we can write the value for the trigonometric functions of 45°:
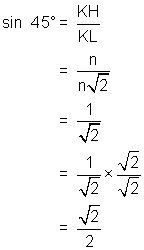
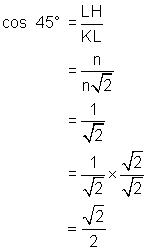
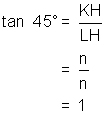
Thus, we have the exact values for the trigonometric ratios of 45°. As a check, use your calculator to evaluate
and sin 45°. You should note that they give the same value. It is left to you to determine the exact values of the trigonometric ratios of angles for which 45° is the related angle (135°, etc.) The only difference in the values for them will be their sign and this will depend on the quadrant in which they are found.
Next we will determine the exact values of the trigonometric ratios of 30° and 60 ° .
To determine the exact values of the trigonometric ratios of 60° and 30° we draw an equilateral triangle and drop the altitude to the base as shown below:
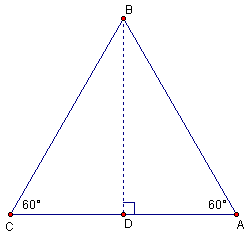
It should be obvious that DBCD @ DBAD (SAS Postualte) . Therefore ÐCBD = 30° and CD = AD. Now let CD and AD be represented by n, and thus CB will be 2n. This is marked on the diagram below:
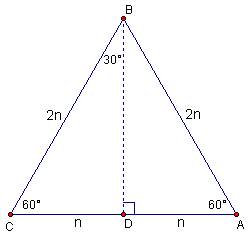
Use DBCD and the Pythagorean Theorem to find BD:
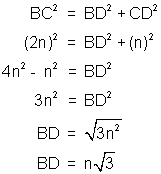
Now use DBCD to find the sine, cosine and tangent of 60° and 30°.
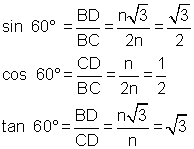
Again, to check our calculations, use your calculator to find sin 60° and the value of
. They should be the same value.
It is left to you to find the exact values of the trigonometric ratios for 30° and to find the exact values for angles for which 60° and 30° are related angles.
Activity
Check Your Understanding p.272 - 274. Complete 6 to 15 inclusive
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
- The point where the terminal arm of an angle in standard position intersects a unit circle has coordinates ( -0.6018 , 0.7986). What is the measure of the angle to the nearest degree?
- The point where the terminal arm of an angle in standard position intersects a circle with centre at the origin has coordinates ( 6 , -8 ). What is the measure of the angle to the nearest degree?
Click here for suggested solution.