Learning Resources
Lesson
This investigation covers materials that is also covered in Mathematics Modeling, Book 2 (M2205) ; you should be able to complete it very quickly. The idea is to see than any co-ordinates of a circle can be expressed as trigonometric functions of the central angle.
To complete the investigation you will require:
- graph paper
- ruler
- protractor
- compass
- scissors
In Step A, the two circles are required; the cut out will be used for measurements and discoveries; the second for recording information.
To fold the circle in sixths for Step B it may be necessary to draw six equal central angles of 60º with your protractor before folding.
Steps C through F are straightforward, simply follow the directions given. Step G and Step H will finish creating four triangles which should be congruent ( check the measurements as requested ).
Step I reinforces your discoveries concerning these triangles. For Step J record your information and estimate the co-ordinates.
Step K and Step L introduces angles in standard position and related angles; make note of these definitions and diagrams. Determine how they are different and how they are alike. Create the table requested and leave room to extend the table by four more columns.
For Step M and Step N use the ratios for the three trigonometric functions given in the side bar to complete the table. Using the estimated co-ordinates from Step J and the ratios you should be able to complete the table; the values will only be approximations. Remember to use the proper signs for each point on its quadrant location. Your values and calculator values should be very close. When using your calculator use the measure of the angle not the related angle measure.
Now that the investigation is complete, consider the following comments regarding this issue.
An angle has two arms which meet at a fixed point called the vertex. We will consider one of the arms to be fixed in place and the other free to rotate. The fixed arm is called the initial arm or initial side and the rotating arm is called the terminal arm or terminal side. This is shown in the diagram below. Click on the point on the terminal side to rotate it.
If we now put this angle on a co-ordinate system with its vertex at the origin and the initial arm along the positive x-axis, we say that the angle is in standard position. This is shown in the diagram below.
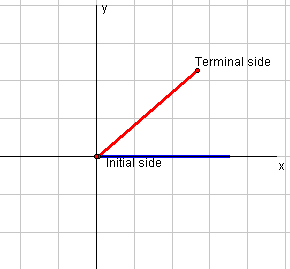
Standard position
We are interested in the co-ordinates of the point where the terminal arm of the angle in standard position intersects a circle whose centre is at the origin of the same coordinate system. This is shown in the diagram below.
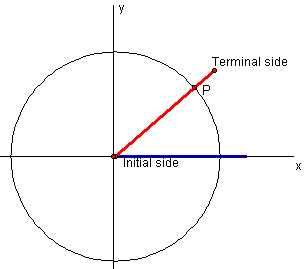
We want to determine the co-ordinates of P. The method of determining these co-ordinates is shown below.
To determine the co-ordinates of point P, construct a perpendicular to the x-axis from P and consider the right triangle so formed. This is shown in the diagram below:
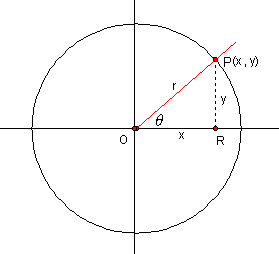
For convenience purposes, small letters are used to denote the sides of the angle and q is used to denote the central angle.
Consider DPOR. From our previous work on trigonometry we know the following:
By multiplying both sides by r we get:
Thus the coordinates of the point where the terminal arm intersects the circle can be given as (r cos q, r sin q). Two things thus affect the co-ordinates of the point. They are the length of the radius and the measure of the angle. This is illustrated by the following example.
Example 1
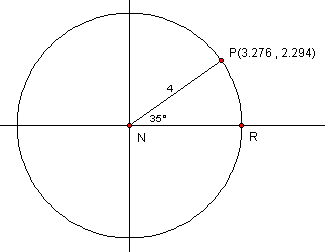
Find the co-ordinates of the point where the terminal arm intersects the circle for the following conditions:
- Radius = 4, central angle = 35°
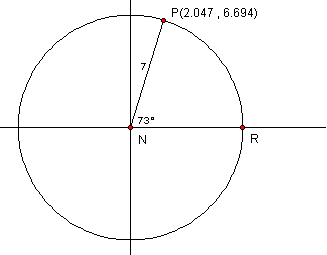
- Radius = 7, central angle = 73°
Solution
- x-co-ordinate = r cos q = 4 cos 35° = 4 (0.8192) = 3.276
y-co-ordinate = r sin q = 4 sin 35° = 4 (0.5736) = 2.294
Note: When using your calculator to find the sine or cosine of an angle, make sure it is set to degrees and not radians. You determine this by pushing the [mode] button and highlighting degrees. - x-co-ordinate = r cos q = 7 cos 73° = 7 (0.2924) = 2.047
y-co-ordinate = r sin q = 7 sin 73° = 7 (0.9563) = 6.694
So far we have only considered an acute angle which has its terminal arm in the first quadrant. We now want to turn our attention to angles whose terminal sides are in the other quadrants.
When we construct the perpendicular to the x-axis from a point where an angle larger than 90° intersects the circle, the triangle formed does not contain the required angle. This is illustrated in the diagrams below. In all of the examples, q the angle in standard position in which we are interested, is not contained in the triangle formed. However, a related angle, a is formed. It is the angle between the terminal arm and the x-axis.
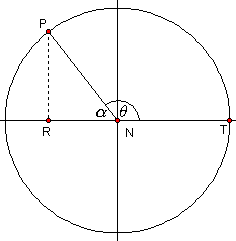measure of related angle a = 180° - q
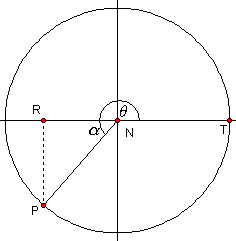measure of related angle a = q - 180°
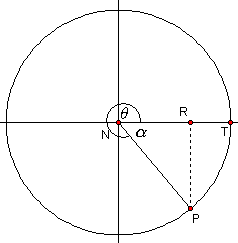measure of related angle a = 360° - q
Example 2
For each case, construct a diagram and indicate on it the angle in standard position and the perpendicular to the x-axis. Then find the related angle and use it to find the co-ordinates of the point where the terminal arm intersects the circle:
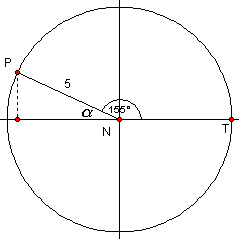
- Radius = 5, central angle = 155°
- Radius = 9, central angle = 228°
- Radius = 3, central angle = 326°
Solution |
Related angle a = 180°-155° r cos a = 5 cos 25° r sin a = 5 sin 25° Since the point is in the second quadrant, the x-co-ordinate must be negative and y-co-ordinate positive: |
2.  |
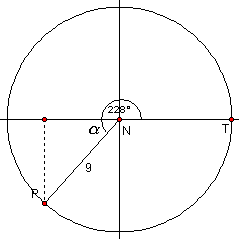Related angle a = 228°-180° = 48° r cos a = 9 cos 48° r sin a = 9 sin 48° Since the point is in the third quadrant, the x-co-ordinate must be negative and the y-co-ordinate must be negative: |
3.  |
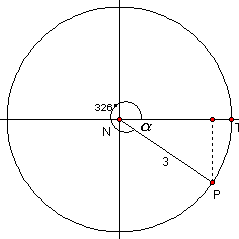Related angle a = 360°-326° = 34° r cos a = 3 cos 34° r sin a = 3 sin 34° Since the point is in the fourth quadrant, the x-co-ordinate must be positive and the y-co-ordinate must be negative: |
Before you go to the activities for this lesson, redo the above examples by substituting the given angles directly in the formulas and calculating the co-ordinates of the points using them instead of first finding the related angle. For example, on your calculator, enter 155° , 228° , 326°. What did you notice? Why then did we bother with related angles? The answer to that will be seen in the next lesson.
Activity
Investigation Questions p.270 - 271. Complete 1, 2, 3, 4 and 5
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
After you do the assigned activities, continue on to the Test Yourself section below for a quick quiz on this lesson.
Test Yourself
An angle of 118° is drawn in standard position. Two circles with centres at the origin are drawn, one with a radius of 4 and another with a radius of 8. Find the co-ordinates of the points where the terminal arm of the angle intersects the circles.
Click here for suggested solution.