Learning Resources
Lesson
So far we have discussed two major forms in which the equation of a circle is usually written. They are:
standard form: ( x - h )2 + ( y - k )2 = r2
general form: Ax2 + Ay2 + Dx + Ey + F = 0
We now wish to consider another form: the transformational form. You have used the transformational form for the equations of other graphs such as the absolute value and parabola. You should recall that the transformational form can be used to tell how a basic graph is translated, reflected, rotated, and stretched. Hence, this form is very useful for graphing purposes.
The basic curve that we are transforming is the unit circle. It is the circle with centre at the origin, radius 1 and equation x2 + y2 = 1. As we have already stated in an earlier lesson, to translate this, or any graph, horizontally h units we simply replace x by x - h, and to translate it vertically k units we replace y by y - k. If we were only concerned with a translation of the unit circle and the radius was not "stretched" the equation would be ( x - h )2 + ( y - k )2 = 1.
You learned in your work in Math 2204 that to "stretch" the graph of any equation (a transformation know as a dilatation) r units in the horizontal direction you multiply the x value by 
. (Note: students who have not completed math 2204 should contact there online teacher about how this transformation works).
Similarly, to "stretch" the graph t units in the vertical direction you multiply y by 
. Applying this to the translated form of the unit circle gives:
However, if we stretch a circle by a different amount in the horizontal and vertical directions it will no longer be a circle. The stretch must be the same in both directions. The transformational form of a circle is thus:
This form tells us that the unit circle is translated h units horizontally and k units vertically. It also tells us that the graph has been stretched by a factor or r. If the unit circle is stretched by a factor of r, the radius of the new circle is r.
It is now a matter of applying this to some problem solving situations.
If you are given an equation in standard form you should be able to convert it to transformational form.
Example 1
Convert 
to transformational form.
Solution
Follow the steps in the interactive window below to view this conversion.
Make particular note that the denominator for the fractional coefficient is the radius of the circle. If the circle is stretched, this denominator changes by a factor equal to the stretch factor.
Example 2
State the transformations of the unit circle that are necessary and then graph the circle with equation: 
Solution
The unit circle is translated 4 units to the right and then 2 units down. Its radius is then stretched by a factor of 6.
Example 3:
Write the equation in transformational form of the the circle below:
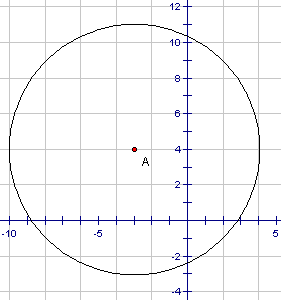
Solution
The centre is at (-3 , 4) and the radius is 7, the equation in transformational form is: 
Activity
Focus Questions p. 263 - 264. Complete 37, 38, 39, 40 and 41
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
After you do the assigned activities, continue on to the Test Yourself section below for a quick quiz on this lesson.
Test Yourself
A circle whose equation is 
is translated 4 units right and 2 units down. Its radius is changed by a factor of 3. Write the equation in transformational form of the new circle .
Click here for suggested solution.