Learning Resources
Lesson
As the topic suggests, we are interested in examining circles under various transformations. The Procedure is based on the given diagram and the idea of moving the circle around on that grid. The steps are self explanatory and you should have no problem to complete the required steps.
In previous work, you learned that in any equation with variables x and y, if x is replaced by x - h the graph is translated h units horizontally. Similarly, if y is replaced by y - k the graph is translated k units vertically.
Keep this in mind as you complete the investigation. For Step F, the centre of a circle is often denoted by (h, k) rather than 
.
The equation of circle with centre at the origin can be written as x2 + y2 = r2, where r is the radius. For example, the equation x2 + y2 = 50 is a circle with centre (0 , 0 ) and radius 
.
In previous work, you learned that in any equation with variables x and y, if x is replaced by x - h the graph is translated h units horizontally. Similarly, if y is replaced by y - k the graph is translated k units vertically.
If we combine the two ideas above, we should be able to write the equation of a circle whose centre is not at the origin. We would expect the graph of the equation ( x - h)2 + (y - k)2 = r2 to be a translation of the graph of x2 + y2 = r2.
To test the above idea, complete the investigation in the interactive window below. (Only the Go forward one frame and Go to beginning global buttons are active) The equation of the graph we start with is x2 + y2 = 16. Note its centre and radius. Click on the arrows to see to where the graph will be translated when x and y are replaced by x - h and y - k.
From the investigation on the previous page, it seems reasonable to state that the equation of a circle with centre (h , k) and radius r can be written as:
( x - h )2 + ( y - k )2 = r2
The above form of the equation is referred to as the standard form of the equation of a circle.
Example 1
A circle whose equation is ( x - 5)2 + (y + 6)2 = 49 is translated 3 units to the left and 5 units up. Write the equation of the new circle. Write the mapping rule that maps the unit circle to the new circle.
Solution
First find the centre and radius of the original circle: centre (5 , -6) , radius = 7. Now translate the centre: 3 units left of 5 is 5 - 3 or 2; 5 units up from -6 is -6 + 5 or -1. The centre of the new circle is thus at (2 , -1) and the radius has not changed. To see this translation use the interactive window below:
The equation of the new circle is: ( x - 2)2 + (y + 1)2 = 49
The rule to map the unit circle into this new circle is:
(x , y) 
(7x + 2, 7y - 1)
(Recall the general mapping rule for a circle is where the point 
is a point on the unit circle and 
is the centre of the image circle and r is the radius of the image circle.)
Example 2
Graph the circle with equation: ( x + 3)2 + (y - 1)2 = 16
Solution
The centre of the circle is at (-3 , 1) and the radius is 4. Use this to draw graph with a set of compasses.
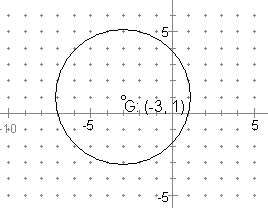
You should now be able to complete the work assigned for this lesson. Before you go to the top of the page and click the Activities button, read carefully the material in the sidebar on page 255 of your text. It summarizes a lot of what we have done with circles and you should copy it in your notebook for easy reference.
Activity
Investigation Questions p.255. Complete 7, 8, 9, 10 and 11
Check Your Understanding p.255 - 257. Complete 12 to 20 inclusive
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
After you do the assigned activities, continue on to the Test Yourself section below for a quick quiz on this lesson.
Test Yourself
A circle has equation: ( x - 2)2 + (y + 3)2 = 25
- What are the coordinates of the centre and length of its radius?
- Draw its graph.
- Write the equation of the circle found by translating this circle 5 units to the left and 4 units up.
Click here for suggested solution.