
Learning Resources
Lesson
As the purpose for this investigation in your textbook points out, you want to find an equation to represent a circle using co-ordinate geometry. To do this a specific example is given to work through. For this investigation you will require
- graph paper
- rulers
- scissors
- compasses
- protractors
This can easily be done individually or if you have a partner it is good for discussion of your results.
We now wish to establish the form of an equation for a circle. We will start with the simple case of a circle with centre at the origin. Later, we will transform this graph and see what happens to the equation. However, for now, let's work with a circle with centre at the origin.
What we are looking for is an equation that gives the relationship between the x and y co-ordinate of any point on a circle. In the diagram below, this means how x is related to y:
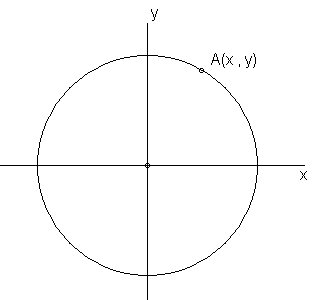
Begin the investigation, complete the steps as directed.
Steps A and B are straightforward. Select a point on the circle that has co-ordinates which are integers since these are easier to work with and any other points can only be approximated and not give accurate answers. The points may be found algebraically as well; click here to view the necessary calculations
In Step C, you will quickly identify CA as the hypotenuse of a right triangle; AB vertical and CB horizontal are perpendicular segments. In Step D, the radius is easily identified to be the hypotenuse of the right triangle and the legs can be represented as x for CB and y for AB . Why? See the Think About in the sidebar of your text and the diagram below.
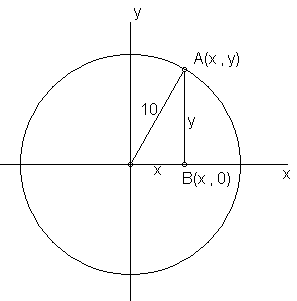
Since this a right triangle, apply the Pythagorean theorem to the sides to obtain the relationships for Step E. Repeat the above procedures in Step F. Write an equation to represent this circle and a circle in general for Step G; use the relationship found in Step H.
Do not continue past this point until after you have completed Steps A to H of Investigation 6 on page 252 in your text.
In the investigation you should have determined that the form for the equation of a circle with centre at the origin and radius r is:
x2 + y2 = r2
To investigate as many examples of this equation as you wish, view the following interaction using Geometers Sketch Pad. Remember, once you have started to do the investigation, the diagram may get messed up. If it does, to return to the original screen you started with, simply press r. This will restore the screen to the original diagram. When you are finished with the investigation, simply click the [back] button to returned to this page.
To investigate as many examples of this equation as you wish, view the following interaction using Geometer's Sketch by clicking here
To determine if a given point is inside, on, or outside a circle, we have to determine its distance from the centre of the circle and compare it to the radius of the circle.
Example 1
Where is the point A(5 , 3) in relation to the circle with equation x2 + y2 = 36?
Solution
The circle with equation x2 + y2 = 36 has centre at the origin and radius 6. The distance from A to the centre (0 , 0) is:
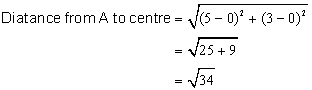
Since ![]() , the point is inside the circle.
, the point is inside the circle.
We now want to consider the equations we have been studying as transformations of the unit circle which has equation x2 + y2 = 1. What we are doing is stretching this basic graph both vertically and horizontally by a factor which corresponds to the radius of the circle. If we only stretch in one direction, either vertically or horizontally but not both, the figure is no longer a circle. We will explore this situation in a later lesson.
Example 2
Describe x2 + y2 = 144 in terms of a transformation of the unit circle and write the mapping rule for the transformation:
Solution
Since the equation is x2 + y2 = 144, the radius is 12 and the unit circle is stretched both horizontally and vertically by a factor of 12. We can write the mapping rule as follows: ![]() .
.
You should now be ready to do the work associated with this lesson.
Activity
Investigation Questions p.253. Complete 1 and 2
Think About p.252 and p.253
Check Your Understanding p.253. Complete 3, 4, 5 and 6
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
After you do the assigned activities, continue on to the Test Yourself section below for a quick quiz on this lesson
Test Yourself
The equation of a circle is x2 + y2 = 65
- What are the coordinates of its centre and the length of its radius?
- Sketch the circle on grid paper.
- Where is the point (5 , 6) in relation to the circle?
- Describe the circle in terms of a transformation of the unit circle and write the mapping notation for it.
Click here for suggested solution.