Learning Resources
Lesson
Up to this point, we have been proving the tangent properties either formally by the Euclidean method or inductively with paper folding. We can also illustrate specific examples or prove generally these properties by using co-ordinate geometry.
Following the method of the Focus, you will need graph paper and a set of compasses.
In Step A, make sure you open your compasses to a width of 13 squares on the graph paper and draw the circle from (0 , 0). Note to check the circle is correct it should pass through the points (13 , 0), (0 , 13), (-13 , 0) and (0 ,-13).
If you were to draw a right triangle by dropping a perpendicular from the point
(12 , 5) to the x-axis, you would see that its hypotenuse is 13 (using the Pythagorean Theorem); which is the radius of the circle.
Step B requires you to find the slope of the radii drawn to Q(5,12) and R(12,5) .
To determine the slope of these radii, use rise over run between the points on the graph itself or the slope formula:
One point will be the end point of the radius and the other point will be the centre of the circle (0 , 0).
For Step C and Step D, the equation of a line has to be found. Recall the use of the point-slope form for a linear equation from your previous work in mathematics; the formula is given in the sidebar of your text book. When a line is perpendicular to the radius, it will have a slope that is the negative reciprocal of the slope of radius. For example: if the slope of the radius is 
then the slope of the line perpendicular is 
; if the slope of the radius is 
then the slope of the perpendicular is 
.
To find the equation of a line you will have to recall the use of the point-slope form. For example, if the slope of a line is and passes through the point 
, then substitute for m and 6 for x1 and 5 for y1 to obtain the standard form of the linear equation.
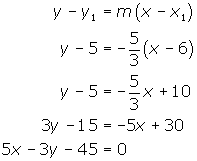
In Steps B and C determine the slope of each perpendicular to the radii for the given points and use the above method to find the equation of each line.
You should be able to easily answer the questions ins Step E.
Step F requires you to find the intersection point of two lines for which you know the equations. One method of doing this is to read the co-ordinates of the point of intersection directly from the graph. This is the best method when the coordinates are integers. However, when the coordinates are not integers they are difficult, if not impossible, to read from the graph.
To find the coordinates of the point of intersection of any two lines for which we know the equations we can solve the system of equations algebraically by a number of different methods that you studied in an earlier course; substitution, elimination or matrices. Use whichever method you are most comfortable with to answer the question in this step.
An example of solving a system using substitution is given:
Example
Find the point of intersection of the following two lines:
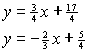
Solution
Use the substitution method:
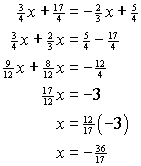
This means that the x-coordinate of the point of intersection of the two lines is 
. To find the y-coordinate of the point we must substitute this value into one of the original equations:
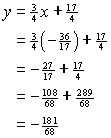
Thus the y-coordinate of the point of intersection is 
and the point of intersection is 
In Step G, use the distance formula 
to calculate the distance from Q to A and then from R to A. What do you notice?
The conclusion in Step H (which we have already determined by several other means) is: The intersection point of two tangents is equidistant from their respective points of tangency.
Activity
Check Your Understanding p.249 - 251. Complete 59 to 70 inclusive
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
After you do the assigned activities, continue on to the Test Yourself section below for a quick quiz on this lesson
Test Yourself
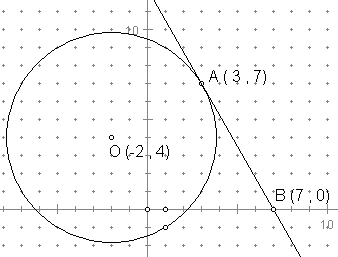
Segment AB touches the circle with centre O(-2 , 4) at point A(3 , 7). The coordinates of B are (7 , 0). From the diagram, it looks like AB might be a tangent to the circle. Prove either that AB is or is not a tangent.
Click here for suggested solution.