
Learning Resources
Lesson
You have already made the conjecture that the tangent to a circle is perpendicular to the radius drawn to the point of tangency by paper folding; now we will use this property in deductive proof. Your text book illustrates a proof (Example 9, page 245) by two methods; Euclidean and transformational. Study both and make sure you understand each step provided. Remember there is more than one way to correctly complete a proof whichever method is used
In this lesson you will do proofs that require the properties of tangents. These proofs will also require many of the other properties about chords, inscribed angles, congruent triangles, etc. that we have discussed so far.
After you are familiar with the various properties, the best way of learning to do proofs is to observe some examples and then to practice doing them yourself. With this in mind, work through the following example. Before you go on to each step in the example, decide what you would have written and compare it to what is presented.
Example
Prove that the segment joining the point of intersection of two common tangents to the centre of a circle bisects the angle between the tangents.
Given: BC and BD are tangents
Prove: Ð ABC @ Ð ABD

To see the proof developed in a step by step fashion click here.
Activity
Check Your Understanding p.246 -247. Complete 52 to 58 inclusive
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
After you do the assigned activities, continue on to the Test Yourself section below for a quick quiz on this lesson.
Test Yourself
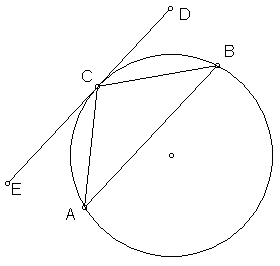
In the diagram below, it is given that ED is a tangent to the circle at point C and AC @ BC. Prove that ED || AB
Click here for suggested solution.