
Learning Resources
Lesson
By constructing examples in this investigation you will discover properties of tangents to a circle inductively (i.e. from examples to conclusions). The term tangent to a circle has already been defined; it is a line that touches a circle at only one point.
You have two methods of exploring the properties presented in this Investigation. One is to use the text book procedure. The other is to use the Geometer's Sketch Pad interactions provided.
Text Method
You may work in pairs, if possible, to complete this investigation such that you may check each others fold lines. The folding must be done accurately to obtain the correct results. For this investigation you will require:
- compasses
- ruler
Be sure to record in your notebook the answer to Step E and Step H. These are properties that you will use in other proofs and calculations. Also, be sure to record in your notebook the answer to Investigation Question 47(f) as this is also an important property that you will use in the future. If you experience difficulty with this method, you can click here for some help and hints.
Geometer's Sketch Pad Method
Once you have started to do the investigation, the diagram may get messed up. If it does, to return to the original screen you started with, simply press r. This will restore the screen to the original diagram. When you are finished with the investigation, simply close the window and you will be returned to this page.
The first interactive window replaces Steps A to E in your text and deals with making a conjecture about the angle formed by a tangent and a radius drawn to the point of tangency. Be sure to record in your notebook the answer to Step E before you go on to the next part of the investigation. You should round the measures of the angles you are investigating to the nearest degree. Click here to start investigating the relation between a tangent and a radius (diameter) drawn to the point of tangency.
The second interactive window replaces Steps F to H in your text and deals with the distance from a point of intersection of two tangents to their respective points of tangency on the circle. Be sure to record in your notebook the answer to Step H before you go on to the next part of the investigation. Click here to start investigating the relation now.
The third interactive window replaces Investigation Question 47(a) - (e) on page 244 in your text and deals with the relation of a tangent chord angle to an inscribed angle intercepting the same arc. Be sure to record in your notebook the answer to 47(f) on page 244 before you go on to the next part of the this lesson. Click here to start investigating the relation now.
If you are sure you understand the properties that were presented in the investigation, you may go to the top of the page and click the activities button to proceed with the work on this lesson. If you are in any doubt about what you should have discovered, read the summary below before you begin.
Summary
1. The angle formed by a tangent line and a radius drawn to the point of
tangency is a right angle: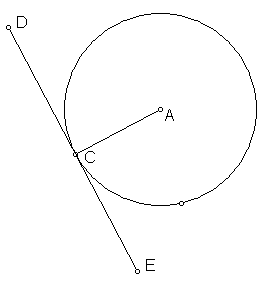
Ð ACE = 90°, Ð ACD = 90°, and AC ^ DE
2. The point of intersection of two tangents to the same circle is equidistant
from their respective points of tangency: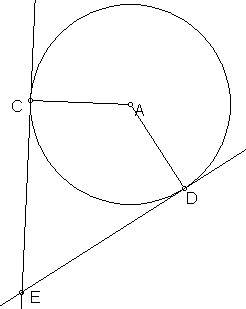
EC = ED
3. The angle between a tangent and a chord is equal to the inscribed angle on
the opposite side of the chord (i.e. intercepting the same arc):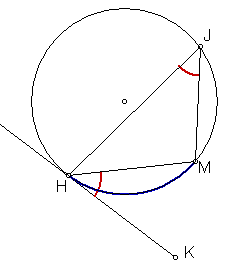
mÐ KHM = mÐ HJM (Hint: Note the arc in blue, it lies in the interior of both the tangent chord angle and the inscribed angle.)
Activity
Investigation Questions p.244. Complete 47
Check Your Understanding p.244 - 245. Complete 48, 49, 50 and 51
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
After you do the assigned activities, continue on to the Test Yourself section below for a quick quiz on this lesson.
Test Yourself
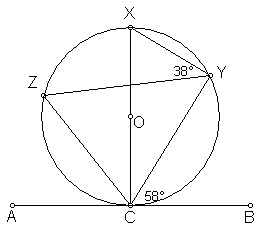
1. In the diagram below, AB is a tangent at C and XC is a diameter.
mÐ YCB = 58° and mÐ XYZ = 38°.
Find the following:
mÐ YXC, mÐ YZC, mÐ YCX, mÐ ZCA, mÐ ZCX, mÐ ZYC,
Click here for a suggested solution.