
Learning Resources
Lesson
In this lesson, instead of doing an investigation and making a conjecture about the properties of arcs, chords, inscribed angles, etc., we will consider some of these same properties (and many new ones) and provide a proof for them.
The only way to become proficient with proofs is to practice writing them and study examples of how they are set up. However, if you do not memorize the properties as you learn them, you will not be able to apply them in future proofs. Before you begin, you might like to quickly review what you have done so far in this Unit.
All of the proofs in the Focus Questions have to be examined and discussed. You should be able to discuss any of these if called upon by your teacher. If you are experiencing difficulty with any of these proofs, seek advice and help; do not leave any of these out since the conclusions obtained will be used in later proofs and applications. As well, note the terminology and the accompanying diagrams in the sidebar of your text book in this Focus; it absolutely necessary that you be familiar with all of these (make sure you know the meaning of the following terms: cyclic quadrilateral, tangent, secant, sector of a circle, and segment of a circle). Add them to your vocabulary notebook.
The proofs can be done by Euclidean proof methods, paper folding or transformational geometry methods or geometry software if you have access to it. Whichever method you choose, you will have to be able to explain your reasoning in any discussion of the problem.
Example 1
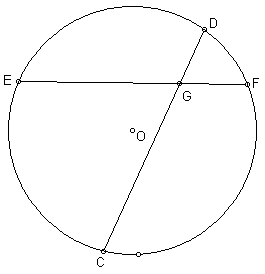
The first example we will do is Focus Question 18 (d) on page 238 in your text. It asks us to prove that an angle formed by two chords intersecting inside a circle is half the sum of the arcs intercepted by the angle and its vertically opposite angle. This is shown in the diagram below
Given:
Chords EF and CD intersecting at point G.
Prove:
m ÐCGE = ½ (m ![]() + m
+ m ![]() )
)
Proof:
To see the proof presented in a step by step fashion click here.
Note that in the above diagram we can also say that:
m ÐDGE = ½ (m ![]() + m
+ m ![]() )
)
In addition to the proofs associated with this lesson, there are applications which require calculations using algebraic and trigonometric relationships. Some of these calculations require formulas that you learned in previous courses. A few of the formulas are given in the sidebars in your text book, the others you will have to recall or look up again. The next section deals with problems of this type.
Example 2
A chord 4.8 cm long is drawn in a circle of radius 3.0 cm. What is the area of the minor segment cut off by this chord?
Click here to see the solution.
You should also be able to do Euclidean proofs and calculations using the properties of chords and arcs.
- You should know the meaning of the following terms: cyclic quadrilateral, tangent, secant, sector of a circle, segment of a circle. Check the definition for these terms in your book.
- You should be able to do Euclidean proofs and calculations using the properties of chords and arcs.
Activity
Focus questions p.238 - 240. Complete 18 to 23 inclusive
Check Your Understanding p.240 - 243. Complete 24 to 46 inclusive
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
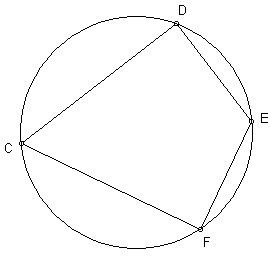
1. In the diagram below, DE @ FE and DC @ FC.
Prove: ![]() @
@ ![]()
Click here for suggested solution.
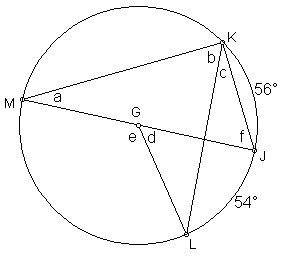
2. In the diagram below, m ![]() = 56° and m
= 56° and m ![]() = 54°
= 54°
Find: a, b, c, d, e, f ( Note G is the centre of the circle )
Click here for suggested solution.