
Learning Resources
Lesson
You have discussed and explored the chord properties in a circle, but an important aspect of any graphic design project involving circles is the properties of angles drawn in the circles. In this investigation you will explore some of these angles and their properties.
Many new terms are introduced and illustrated in this lesson including: minor arc, major arc, subtends, intercepts, inscribed angle, and central angle. These are defined and illustrated with diagrams in your text book. If you need further clarification, click here for further discussion.
The purpose of the investigation is to find the relationship between the central angles and inscribed angles. It is best to work with a partner or in a small group, if possible, with each member of the group drawing circles and angles of various sizes; compare the results found with each other. Be sure to record all results in your own notebook.
To complete the activity you will require
- a ruler
- a set of compasses
- a protractor
- coloured pencils or markers
There are two ways to proceed in this investigation. One is to use the method described in your text, the other is to use Geometer's Sketch Pad in the interactive windows provided in this lesson.
Text Method
Steps A and B introduces terminology and diagrams associated with each term. When naming arcs, especially major arcs, it is a good idea to name them in a clockwise direction such that everyone has the same answers.
Simply follow the directions in your text for Steps C to K. The main thing to record and mark plainly in your note book is the answer to Steps G, J, and K.
Geometer's Sketch Pad Method (replacing steps C to F)
For the first part of the investigation, open the window and click on point A. Drag A to several locations and record the measure of the central and the inscribed angle. After you have made these observations, use them to answer Step G of the Investigation on page 234 in your text. Record you answer in your note book.
Once you have started to investigate the different positions for A, the diagram may get messed up. If it does, to return to the original screen you started with, simply press r. This will restore the screen to the original diagram. When you are finished with the investigation, simply close the window and you will be returned to this page.
Click here to start investigating the relation between an inscribed angle and the arc that subtends it.
Geometer's Sketch Pad Method (replacing steps H and I)
The next part of the investigation is to discover a relation between two inscribed angles that intercept the same arc. Again open the window and drag A or B to several locations and record the measure of the two angles. After you have made these observations, use them to answer Step J of the Investigation on page 234 in your text. Record your answer in your note book.
In the investigation which follows, both inscribed angles intercept the same arc. Click here to start investigating the relation between an inscribed angle and the arc that subtends it.
Geometer's Sketch Pad Method (replacing step K)
The final part of the investigation is to discover a relation about an inscribed angle which intercepts a semi-circle. After you have made your observations, use them to answer Step K of the Investigation on page 234 in your text. Record your answer in your note book.
Click here to start investigating an angle inscribed in a semi-circle.
After you have finished your investigations, either by using the text method or the GSP method, continue below for a summary.
Summary
- A minor arc is an arc with a measure less than 180° and a major arc is an arc with a measure greater than 180°.
- An arc with a measure of 180° is a semi-circle.
- The measure of an arc is equal to the measure of the central angle it subtends.
- An inscribed angle is half the measure of the arc it intercepts and therefore half a central angle intercepting the same arc.
- Inscribed angles intercepting the same arc have equal measures.
- An angle inscribed in a semi-circle is a right angle.
You should print off the above definitions and put them in your notebook or binder for future reference.
Activity
Investigation Questions p.234 - 236. Complete 1 to 11 inclusive
Think About p.232
Check Your Understanding p.236 - 237. Complete 12 to 17 inclusive
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
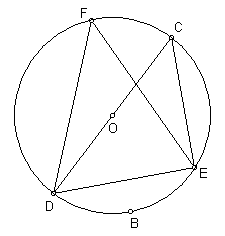
1. Given: In the diagram below m![]() = 96° and DF = EF. Find: mÐ CDF, m Ð CEF, and mÐ CDE
= 96° and DF = EF. Find: mÐ CDF, m Ð CEF, and mÐ CDE
Click here for suggested solution.