Learning Resources

Investigation 4: Angles and Arcs

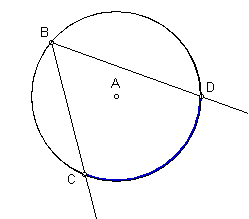
Associated with every arc there is a central angle. A central angle is an angle with vertex at the centre. If the sides of the angle pass through the end points of the arc, we say the central angle intercepts the arc and the arc subtends the angle. This is illustrated in the diagram below.

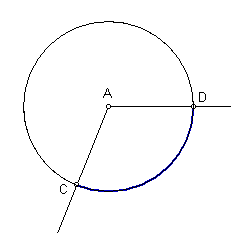
In the diagram above  ÐCAD is a central angle and its sides contain points C and D, the endpoints of the . We therefore say that  subtends ÐCAD and ÐCAD intercepts . Notice that the arc is in the interior of the angle.

By definition, the measure of an arc is equal to the measure of its central angle. The measure of an arc is thus given in degrees. In the above diagram we would use the following notation to write the measure of the arc: 
                                               m= mÐCAD

Any angle can intercept an arc, but only the central angle has measure equal to the arc. Consider the diagram below.  All three angles, ÐCVD, ÐCYD, and ÐCAD intercept the arc, but only ÐCAD has measure equal to the arc.

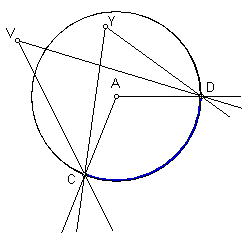
It is also important to note that an arc is measured in degrees and not in centimetres or some other unit of length. The measure of an arc and the length of an arc are two totally different things and this is indicated in the diagram below.

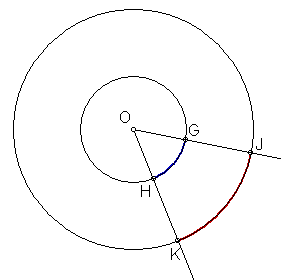
In the above diagram because they both subtend the same central angle at O. However, it is fairly obvious that the distance from H to G measured along the arc is not the same as the distance from K to J measured along the arc. Arc length depends on both the central angle AND the length of the radius. In this lesson we are only interested in the measure of the arc not its length. In this lesson we are only interested in the measure of the arc not its length. Click here for a paper folding activity to illustrate this idea if you are certain of the difference.

We have to consider one more special angle before we begin our investigation called an inscribed angle. By definition, it is an angle whose vertex lies on a circle and whose arms are chords of the circle. It is shown in the diagram below. We say ÐCBD is an inscribed angle which intercepts . We can also say that  subtends ÐCBD.