Learning Resources
Lesson
In this lesson there are no new concepts. You will combine the work you did on circles and chords with the work you did on co-ordinate geometry. The work is a straightforward application of the distance, midpoint and slope formulas to various examples dealing with chords in a circle.
To help you with this work, study these examples.
Example 1
A circle has centre at the origin and a radius of 
. Are the points A(6 , 3) and B(-3 , 6) inside, on, or outside the circle? If they are on the circle, show that the segment from the centre to the mid-point of AB is perpendicular to AB.
Example 2
Prove using co-ordinate geometry that the diagonals of a square are perpendicular.
Solution
To prove this in a general case, draw a square on a co-ordinate plane with one vertex at the origin and the sides aligned with the axes such that one vertex is on the x axis and one on the y axis. If we let each side of the square be a units then the diagram below would represent the situation.
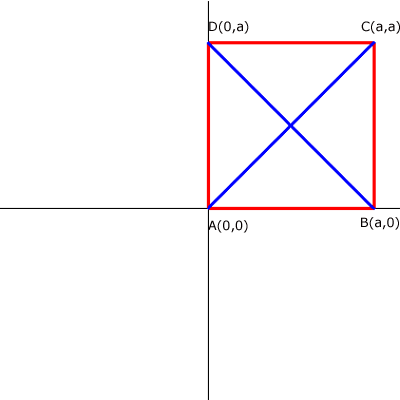
Finding the slope of each diagonal we have
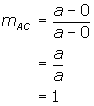
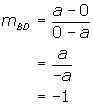
Since the slopes are negative reciprocals, the diagonals are perpendicular.
After you have studied the solutions for these examples, go to the next page for a summary of how to do proofs using coordinate geometry.
Summary
- To prove segments are congruent, calculate their length using the distance formula and show that they are equal.
- To prove segments bisect each other, show that they have the same midpoint.
- To prove segments parallel, show that they have the same slope.
- To prove segments perpendicular, show that their slopes are negative reciprocals of each other.
Activity
Focus Question p.230. Complete 28
Check Your Understanding p.230 - 231. Complete 29 to 37 inclusive
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
After you do the assigned activities, continue on the Test Yourself section below for a quick quiz on this lesson.
Test Yourself
A circle with centre E(-5 , 3) passes through points F(3 , 9) and G(-5 , 13).
- What is the length of the radius of the circle?
- What is the distance from the centre to FG?
Click here for a suggested solution.