
Learning Resources
Lesson
This Focus is concerned with finding the distance between co-ordinate points; this is done in the context of the sports complex problem. To determine the distance from B to C , a vertical distance, on the given diagram is a simple matter of counting the blocks; however, algebraically it is the difference of the y-co-ordinates of the points. Similarly the distance from B to E , a horizontal distance, is the difference of the x-co-ordinates.
Following Example 5 in your text book, you will have a process of finding the distance between two points that are not on the same vertical or horizontal line (i.e. the line segment is oblique)
If we are given two points, A(x1 , y1) and B(x2, y2), can we develop a formula that will give us the distance between them? Alternately we could say we are looking for a formula for the length of the segment that has these end points. To see the development of a formula, commonly referred to as the distance formula, click here.
A second concern of this Focus is to discover a means of finding the co-ordinates of the midpoint of a line segment. Using the points A(x1 , y1) and B(x2, y2) we can find a formula that will give us the co-ordinates of the midpoint of the segment. To see the development of this formula, commonly referred to as the midpoint formula, click here. A means to recall this formula is to think of the midpoint as having co-ordinates that are the average of the co-ordinates of its endpoints.
Once you have seen where the formulas come from, the next step is to apply them to solving problems.
Example 1
Given the quadrilateral CDEF with vertices C(-10 , 3), D(-7 , 11), E(1 , 14), and F(-2 , 6). Show that CDEF is a rhombus and that its diagonals bisect each other (i.e., have the same midpoint).
Solution
The first thing with any problem involving co-ordinates is to plot the points on a grid:
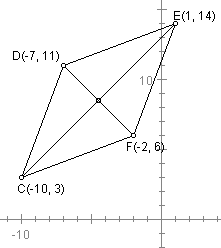
By definition, a rhombus is a quadrilateral with four equal sides. Use the distance formula to calculate the length of each side:
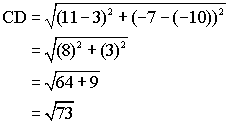
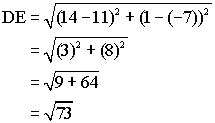
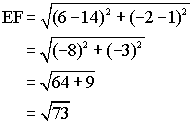
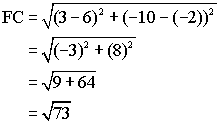
Since all four sides have length ![]() they are equal and the quadrilateral is a rhombus.
they are equal and the quadrilateral is a rhombus.
Now check the midpoints of the diagonals. If the diagonals have the same mid-point, then they bisect each other.
Mid-point of CE Mid-point of DF
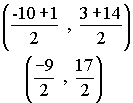
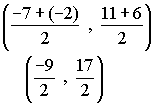
Thus CE and DF bisect each other.
Summary
Given points P(x1 , y1) and Q(x2 , y2), then:
The length of PQ, or the distance formula , is:
![]()
The mid-point of PQ, or the mid-point formula is:
![]()
Activity
Focus Questions p.226 - 227. Complete 10 to 15 inclusive
Think About p.226 and p.227
Check Your Understanding p.227 - 229. Complete 16 to 27 inclusive
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
Given a triangle with vertices J(-5 ,-8), K(9 , 8), L(1 , 15):
- Is the triangle a right triangle?
- What are the coordinates of the mid-point of its longest side?
- What is the distance from the mid-point of its longest side to the three vertices? What do you notice about the distances?
Click here for suggested solution.