
Learning Resources
Lesson
In earlier lessons, we explored the properties of chords in a circle. From the investigations we did, we made conjectures - statements that we thought to be correct. However, that is all we can say from an investigation - that something looks to be true. We cannot be certain that our conjecture is always true for every case unless we provide some sort of deductive proof for it.
In example 4 on page 218, a deductive proof is given for the conjecture we made about a segment that connects the centre of a circle and the midpoint of a chord. We made a conjecture about this in Investigation 2 and this is a deductive proof that our conjecture was in fact true.
In addition to proving that the conjectures we made in the investigations are true, we can prove other relations about circles using congruent triangle properties; this is what you are asked to do in the assigned exercises. If you would like some extra samples to study before you proceed to the assigned activities, click on the examples below.
Activity
Focus Questions p.219. Complete 27 and 28
Challenge Yourself p. 220
Check Your Understanding p.219 - 221. Complete 29 to 39 inclusive
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
After you do the assigned activities, continue on to the Test Yourself section below for a quick quiz on this lesson.
Test Yourself
Given: Ð CAD @ Ð EAF Prove: CD @ EF |
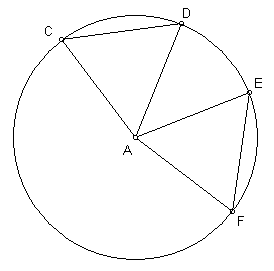 |
Click here for suggested solution.