Learning Resources
Lesson
This Focus is provided as a review of congruent triangles. It may have been quite some time since you encountered these ideas so take your time and study the given examples. In particular spend some time with the congruence theorems and make sure you understand what they mean. Make note of the symbol for congruence recalled for you in the sidebar of your text (p.212) . The symbol ![]() is traditionally used as indicated to state that two geometric figures are congruent to each other.
is traditionally used as indicated to state that two geometric figures are congruent to each other.
In doing the proofs, it is a good strategy to look at what you are trying to prove and work backwards towards what you are given. Examples of both Euclidean and transformational proofs are shown; work with what you feel most comfortable. As well, don't be intimidated by the formal structure of proofs since less formal reasoning is also acceptable.
The sidebar on the pages of this Focus reviews many of the geometric ideas and concepts that you need to know. Make note of the definitions and add to your notebook as you progress through the material.
If two triangles are congruent, what can we conclude?
We want to be able to complete the statement: "If two triangles are congruent then ????"
That is the statement we will focus on in the first part of this lesson. By definition, any two figures are congruent if they are identical in shape and size. For triangles this means the three corresponding/matching sides are congruent AND the three corresponding/matching angles are congruent.
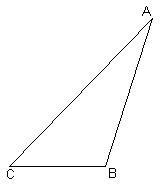
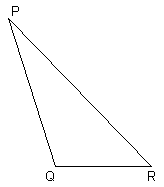
Consider the two triangles below:
|
|
If D ABC @ D PQR then |
|
Sides are congruent |
Angles are congruent |
Now we want to consider the converse of the opening sentence and this is done on the next page.
What information is necessary to conclude that two triangles are congruent?
We want to be able to complete the statement: " If in two triangles ????, then the triangles are congruent."
From the definition of congruence on the previous page and also in the margin on page 212 of your text book, we can say the following:
If in two triangles the three corresponding sides are congruent AND the three corresponding angles are congruent, then the triangles are congruent.
Thus if six pieces of information are known (the three sides AND the three angles) we know by definition that the triangles are congruent. However, it is not necessary to have all six pieces of information. In fact, to conclude that triangles are congruent, we only need 3 pieces of information, not 6, provided they are the correct three pieces.
What three pieces do we need?
First consider three pieces of information that would not be sufficient to say two triangles are congruent. Knowing only the three angles would not be sufficient as is shown in the diagram below:
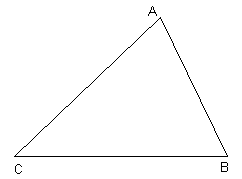
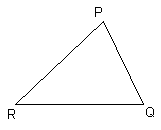
ÐA @ ÐP, ÐB @ ÐQ and ÐC @ ÐR but DABC is NOT congruent to DPQR as they are obviously not the same size.
There are five different possibilities for the three pieces that are sufficient and necessary to prove triangles are congruent; these are shown quite nicely in your text on pages 212 & 213. You should study these and make sure you understand each; however, you will not be asked to reproduce these. Only one of these five is discussed in detail here. For the other possibilities, all of which are called postulates, go to page 213 in your text.
(Note: A postulate is something that is assumed to be true, usually because it is intuitively obvious. It is then used as a basis for argument in a logical reasoning process or proof.)
The Side-Side-Side Congruency Postulate (SSS)
This postulate states that if the three sides of one triangle are congruent to the matching three sides of another triangle, then the triangles are congruent. We have only three pieces of information, viz. the three sides and we are claiming that is sufficient to conclude the triangles are congruent. In other words, if the three sides are congruent, then the three angles must also be congruent since the triangles are congruent.
Let's construct a triangle whose three sides are congruent to the corresponding three sides of a given triangle and see if in fact the angles turn out to be congruent. To view that construction click here.
The other postulates are referred to as the SAS, ASA, SAA, and HL postulates. They are discussed on page 213 in your text. Don't be too concerned about a justification similar to what we have just done for these postulates. It is more important to know what they say and be able to apply them to other proofs. It is the application of these postulates to which the rest of this lesson is devoted.
In your text book on pages 214 and 215 are several examples of how these postulates can be used to prove new properties and facts about triangles. Read them carefully before beginning the assigned activities.
Two other examples are done in this lesson to serve as a guide for the assigned work. Simply click on each example in turn to see the presentation.
Summary
In this lesson you were introduced to and should now have a thorough understanding of the following:
- SSS Congruency Postulate:
If the three sides of one triangle are congruent to the three sides of a second triangle, then the triangles are congruent. - SAS Congruency postulate:
If two sides and the included angle of one triangle are congruent to two sides and the included angle of a second triangle, then the triangles are congruent. - ASA Congruency Postulate:
If two angles and the included side of one triangle are congruent to two angles and the included side of a second triangle, then the triangles are congruent. - SAA Congruency Postulate:
If two angles and a non-included side of one triangle are congruent to two angles and a non-included side of a second triangle, then the triangles are congruent. - HL Congruency Postulate:
If the hypotenuse and a leg of one right triangle is congruent to the hypotenuse and a leg of a second right triangle, then the triangles are congruent. - Proof:
Be able to apply all the congruency postulates to prove or justify other properties about triangles.
Activity
Focus Questions p.216 - 217. Complete 22, 23 and 24
Check Your Understanding p.217. Complete 25 and 26
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
After you do the assigned activities, continue on to the Test Yourself section below for a quick quiz on this lesson.
Test Yourself
Given: FC || ED FC = ED AB = CD
Prove: FA || EB |
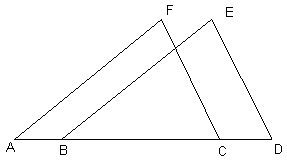 |
Click here for suggested solution