Learning Resources
Lesson
In this lesson, two examples of natural phenomena that are measured using a logarithmic scale are studied; earthquake intensity and sound intensity.
Logarithms were introduced and derived by a Scots mathematician, John Napier, approximately 400 years ago. At the time, this was a great discovery since it reduced the operations of multiplication and division to addition and subtraction by using the laws of logarithms as derived by Napier. Extensive tables for common logarithms were written and recorded to facilitate these computations - of course, calculators and computers have made this application obsolete today.
Napier originally worked with a binary sequence
1, 2, 4, 8, 16, 32, ...
which could be expressed as
20, 21, 22, 23, 24, 25, ...
the exponents then became the base 2 logarithms of the numbers which can be summarized as follows:
Number (N) |
20 |
21 |
22 |
23 |
24 |
25 |
... |
Exponent ( |
0 |
1 |
2 |
3 |
4 |
5 |
... |
)The row of logarithms is known as a logarithmic scale. As the sequence increases by a factor of 2, the exponent only increases by 1.
Today, logarithmic scales are commonly built on the powers of 10
Number (N) |
100 |
101 |
102 |
103 |
104 |
105 |
... |
Exponent ( |
0 |
1 |
2 |
3 |
4 |
5 |
... |
)In this table as the numbers increase by a factor of 10, the exponents increase by 1. This logarithmic scale is used to describe many natural phenomena.
Read and study the descriptions given for the logarithmic scales for earthquakes and sound. For further examples, go to the next page.
Consider the following examples :
Example 1
A recent earthquake that occurred in Alaska had a magnitude of 5.7 on the Richter Scale. An earlier one had a magnitude of 6.9. How many more times intense was the earlier earthquake?
Solution
Using the formula given in the text , the earlier quake has 
. Let I1represent the intensity of this quake. Note 
as the reference intensity.
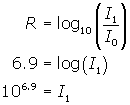
Using the formula given in the text , the recent quake has 
. Let I2represent the intensity of this quake. Note as the reference intensity.
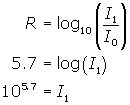
To determine the number of times of intensity that the earlier quake is then the most recent divide them
The earlier earthquake was 15.8 as intense as the most recent earthquake.
Example 2
Two loud TVs are playing simultaneously in a Department store at 80 dB each. What is the decibel level of the two sets together?
Solution
From the text book discussion
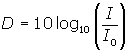
where I0, the reference sound is 10-12 . Also the table in your text gives the intensity level for 80dB to be 10-4 W/m2 .
The intensity for two sets will be twice the intensity of 1 set.
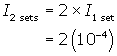
Using the formula find the decibel level for this intensity.
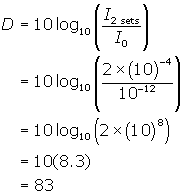
The two sets will have 83dB level.
Activity
Focus Questions p.187. Complete 33, 34 and 35
Think About p.185 and p.187(2 items)
Check Your Understanding p.187 - 188. Complete 36 to 43 inclusive
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
After you do the assigned activities, continue on to the Test Yourself section below for a quick quiz on this lesson.
Test Yourself
The acidity of rainwater is measured with a logarithmic scale called a ph scale in which 1 unit decrease in the ph level represents a 10 fold increase in acidity. The ph level is given by
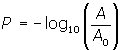
where A represents the acid of substance with a ph of P and A0represents the acid content with ph of 0.
A lake near the TCH in Newfoundland has a ph of 4.0. How many times as acidic as clean rainwater, which has a ph of 5.6, is the water in the lake?
Click here for suggested solution.