Learning Resources
Lesson
The Focus in this lesson gives you the opportunity to apply the laws of logarithms to more complex exponential equations. You should read and study Example 10 and 11 found in your textbook (p.178-9) and make sure you understand each step in the solutions. If you have a good understanding of finding exponential equations from earlier lessons in this unit and the laws of logarithms, you should be able to work through all of the problems and exercises.
The basis of many of these problems is the exponential equation of the form 
; especially when b = 10. The Think About on p.179 asks you to consider how the functions 
and 
. If you recall, it is simply a horizontal stretch. Look at the graphs below of 
(black curve) and 
(red curve).
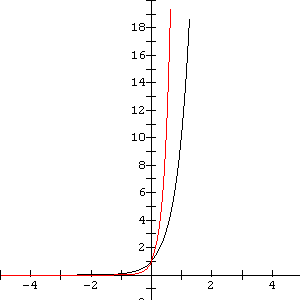
Many of the applications will have this concept embedded into its solution.
If you require further examples to read and study, go to the next page. It is very important that you complete the entire Activities Section to obtain a clear understanding of how to apply these concepts to real-world situations.
Example 1
Vivian is testing a new antiseptic to be used in the hospital. At t = 0 min, 100% of the bacteria are present on the test surface. Eighty minutes after the mixture of ethanol and acetone (i.e. antiseptic) is applied to the test surface, only 38% of the bacteria remain. Assuming that the percentage of bacteria remaining decays exponentially with time, determine when 15% of the original population of bacteria will remain.
Solution
The exponential form 
will model this problem.
The initial amount ( a = 1.00 ) is 100%; eighty minutes ( c = 80 ) after mixture is applied is 38% ( b = 0.38) of the bacteria remain. We have a basic bacteria population described by
where P is the population after time t.
Since the population that remains is 15% of the original, let P equal 0.15 and solve for t .
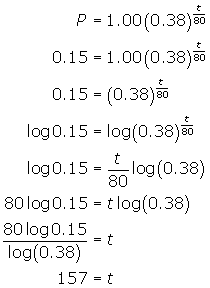
The bacteria population will be 15% of the original 157 minutes or 2 hours and 37 minutes after the initial time.
Example 2
The healing of skin wounds can be modelled using an exponential function. At t = 1day, Amanda's wound was 18 cm2. At t = 3.5 days, the same wound was 14.1 cm2 .
- What was the original size of the wound?
- How large was the wound when t = 5 days?
- When will the wound be 8 cm2?
Solution
(a)
The equation that models this problem will be of the form where x is the time in days for healing of the wound and y is the area or size of the wound. Since no initial size is given , model the two situations; solve for a and equate to find the value of k.
For x = 1 day the wound is 18 cm2
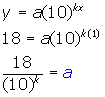
For x = 3.5 days the wound is 14.1 cm2
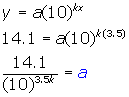
Since a, the initial size of the wound, is the same regardless of time, equate the two expressions and solve for k.
Substitute into either of the expressions for a to find the initial or original size of the wound.
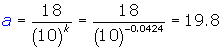
The wound was originally 19.8 cm2 ; the equation that would model the healing of the wound is 
. Note the exponent is negative in this situation since it is a decay curve; the size of the wound is reducing as time passes.
(b) At t = 5 days , the wound will be
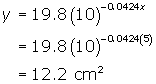
(c) To find the time when the wound will be 8 cm2 , substitute 8 for y and solve for x.
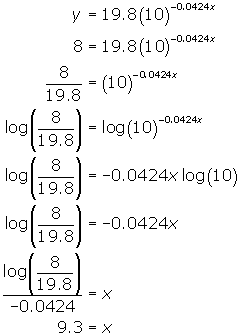
It will take 9.3 days to reduce to 8 cm2 .
The use of the logarithm with base 10 which is found on all scientific calculators is referred to as taking the common logarithm of a value.
The laws of logarithms can be used to solve equations containing either exponents or logarithms. Study the following examples to make sure you understand how to solve these equations. You should note the variable can be found as the argument, the base or the value of the logarithm. Be creative in your use of the laws and the algebra skills that you have since these examples will not cover all the possible situations that you will find in the Activities Section.
Example 3
Solve for x each of the following equations:
(a) 
(b) 
(c) 
(d) 
Solution
(a) Use the Laws of Logarithms to rewrite the left side.
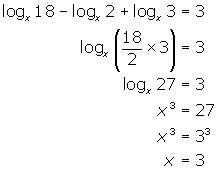
(b) Convert to exponential form and solve:
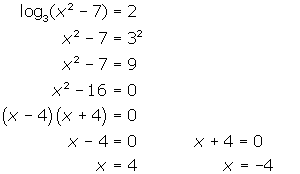
(c) Take the common logarithm of each side and solve:
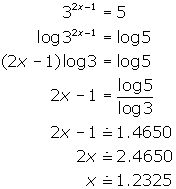
(d) Use Laws of Logarithms to rearrange equation
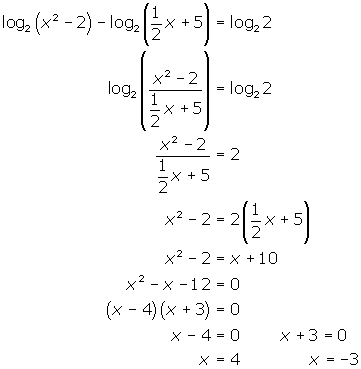
As noted earlier these examples are not exhaustive; you will have to draw on all your algebraic skills to solve many of these problems and equations.
Activity
Check Your Understanding p.180 - 185. Complete 9 to 32 inclusive
Think About p.178,p.180, p.181 and p. 184
Challenge Yourself p.184
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
After you do the assigned activities, continue on to the Test Yourself section below for a quick quiz on this lesson.
Test Yourself
- A house in a high growth area was purchased in 1990 has a value of $110 000 in 1995 and by 2002 its value was appraised at $165 000. If the appraised values are increasing exponentially in this area , find the value of the house in 2010.
Click here for suggested solution.
- Solve: (a)
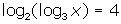
(b)
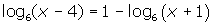
Click here for suggested solution.