Learning Resources
Lesson
The laws of exponents can be used to derive new laws for logarithms. Keep this in mind as you work through the investigation.
As you read and study Step A , look at the Think About in the side bar; this specific case should help you develop the generalization required.
For Step B, repeat the procedure of Step A except this time think about the exponent rule for division with the same base; again refer to the Think About to help develop the required generalization.
Step C requires you to test your conjectures from the first two steps. Working with a partner or small group, create examples for each other to test; use values that are easy to evaluate.
Once you have the rule or law from Step A firm in your mind, you should be able to use it to find the third law of logarithms in Step D. Finally test your conjecture in Step E by creating examples and having your partners work out the solution.
Complete the investigation questions assigned in the Activities Section. If you experience difficulties with the investigation itself, go to the next page for further discussion and clarification of the concepts.
Lets consider the laws of exponents and how they give rise to the laws of logarithms.
Multiplication Law:
How can this be related to the logarithmic form?
If we let 
and 
, then we can write each in logarithmic form as
and 
If we substitute x and y for 
and 
in the multiplication law for exponents and convert it to logarithms we see the following:
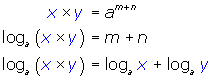
(i.e. the logarithm of a product is equal to the sum of the logarithms of the factors providing the bases are the same throughout)
Division Law:
If we substitute x and y for and in the division law for exponents and convert it to logarithms we see the following:
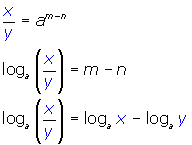
(i.e. the logarithm of a quotient is equal to the difference of the logarithms of the numerator and denominator providing the bases are the same throughout)
Power of a Power:
If we substitute x for in the power of a power law for exponents and convert it to logarithms we see the following:
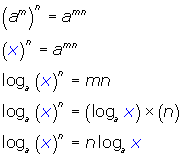
(i.e. the logarithm of a value to a power is equal to the exponent times the logarithm of the value providing the bases are the same throughout)
In summary the three laws of exponents are
- Product Law of Logarithms:
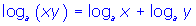
- Quotient Law of Logarithms:
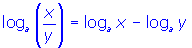
- Power Law of Logarithms:
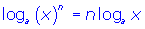
These can be used in various ways to simplify expressions and solve problems. Consider the following examples:
Example 1
Using the laws of exponents, write the following expression as a single logarithm:
Solution
Use the interactive window below and follow each side noting the reasons for each.
In the Investigation Questions an interesting method of solving exponential equations is developed. When the base cannot be made the equal on each side of the exponential equation, you can solve by using the log key on your calculator. Keep in mind that this key represents the logarithm function with base 10 only. In other words, when finding the log x on your calculator you are finding a power of 10 that will give you the argument x.
Example 2
Evaluate 
Solution
This means "find a power of 10 that will give 125" (i.e. 
) The log key on your calculator will give you the solution:
(this means 
)
Since the calculator has base 10 values programmed into it, we can use this solve equations. ( See questions 3 and 4 in the Investigation Questions )
Example 3
Solve for x: 
Solution
Since 17 cannot be expressed as a base 2 with integral exponents, take the logarithms of both sides of the equation. Any base logarithm can be used, but base 10 is the most useful since these are on your calculator.
If we want to evaluate a logarithm with base other than 10, we could change it to its exponential form and follow the above example.
Example 4
Evaluate 
Solution
Let 
and then solve as follows:
Recall, that this solution means that 
. Keep this example in mind as you prove question 6 in the Investigation Questions. This method is known as change of base to evaluate logarithms with bases other than 10.
Activity
Investigation Questions p.177 -178. Complete 1, 2, 3, 4, 5, 6, 7 and 8
Think About p.176( 3 items); p.177 and p.178
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
- Evaluate :
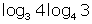
- Solve for x:
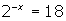
- Write as a single logarithm:
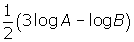
Click here for suggested solutions.