Learning Resources
Lesson
Inverses in mathematics reverses the work that has already been completed. For example, division is the inverse operation to multiplication. The idea of inverses can be applied to functions - the inverse may or may not be a function.
In the Focus questions, it is essential that you read and study the introduction to each . Use technology to complete question 7 such that you can see that one operation is the inverse of the other.
The idea of finding the inverse of a function is found in the idea of interchanging the x and y values. If these values are interchanged, then it is a reflection in the line y = x. Note below the point (1,2) with values interchanged is (2,1) which is a reflection of the point in the line y = x.
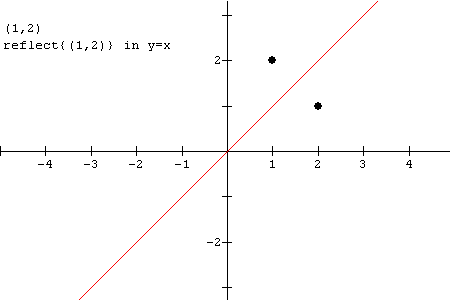
Example 1
Find the inverse of 
by using tables and graph each on the same co-ordinate plane.
Solution
Table of values for
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
y |
|
|
|
1 |
10 |
100 |
1000 |
Table of values for inverse ( x and y interchanged )
x |
|
|
|
1 |
10 |
100 |
1000 |
y |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
The graphs are as follows:
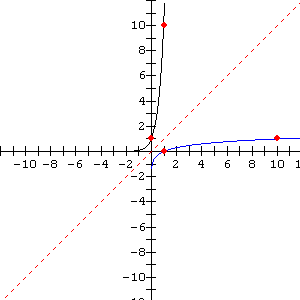
The inverse of (the blue graph) is reflected in the line 
(the red dotted line) as evidenced by the interchange of the coordinates for the marked points.
The equation describing the inverse of would have equation 
since the x and y values were interchanged.
The equation cannot be solved by ordinary algebraic methods. The term logarithm was used to describe this function and is written as
( the 10 is known as the base of the logarithm and the x the argument of the function; as well, the key log on your calculator represents the logarithm with base 10)
In general, then when we have an exponential function of the form 
it can be converted to the logarithmic form 
.(Note that the base of the exponent is the base of the logarithm ; the y value of the exponential form is the argument of the logarithm; and the exponent of the exponential form is the value of the logarithm)
Keep in mind the following points with respect to logarithms:
- A logarithm is written in the form
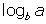, where b is referred to as the base and a is the argument. When one writes 
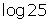, it means 
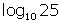. Therefore the log button on your calculator is base 10. - Two relations are inverses of one another if they satisfy these three conditions:
- They are reflections of one another in the line
- The x and y values have been interchanged in the ordered pairs.
- The x and y values have been interchanged in the equations.
Example 1
Convert from exponential form to logarithmic form:
(a) 
(b) 
Solution
(a) will become 
(b) will become 
Example 2
Convert from logarithmic form to exponential form:
(a) 
(b) 
Solution
(a) will become 
(b) will become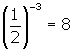 
Example 3
Solve for x:
(a) 
(b) 
(c) 
Solution
(a) Convert the log form into exponential form and solve for x .
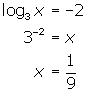
(b) Convert the log form into exponential form and solve for x .
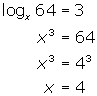
(c) Convert the log form into exponential form and solve for x .
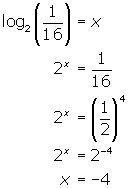
Example 4
Evaluate: (a) 
(b) 
Solution
To answer questions such as this you may be able to do them mentally or have to write them as an equation and solve it in its exponential form.
(a) You should ask yourself "3 to what power will give 27?" since this is what the log form means. Mentally of course the answer or solution is 3.
(b) For this question the answer may not be as obvious : "4 to what power will give 8?" is not so easy as (a) to solve mentally. Therefore, you can write it as a logarithmic equation and change it to its exponential form and solve for x .
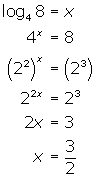
Example 5
Solve for x : 
Solution
You will note that on the right hand side of this equation there are three logarithms that can either be solved mentally or using individual log equations to find the value of x .
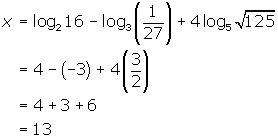
Make sure you understand why each logarithm has the value given in the solution; if you do not understand why each logarithm has the value given, seek help form your teacher or classmates.
Activity
Focus Questions p.173 - 174. Complete 7, 8, 9 and 10
Think About p.173
Check Your Understanding p.174 - 175. Complete 11, 12, 13, 14, 15, 16 and 17
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
After you do the assigned activities, continue on to the Test Yourself section below for a quick quiz on this lesson.
Test Yourself
Write a Journal entry explaining in your own words how exponents and logarithms are related.
1. Convert 
to logarithmic form.
2. Convert 
to exponential form.
3. Evaluate: 
4. Solve for x : 
5. Are these relations inverses? Why or why not?
Click here for suggested solutions.