Learning Resources
Lesson
You have now experienced the full power of exponential functions with exponents that are integral {...,-3,-2,-1,0,1,2,3,...} values. However, we have been drawing graphs for these functions that are continuous and not discrete which means we are assuming that a base can be raised to a power other than integers.
If we use the graph of 
and using the TRACE function on your TI-83 you will find that when x = ½ , the value of y will be 2. Note on the graph below the vertical line through ½ intersects the graph at a point and horizontally from theis point the y value is 2.
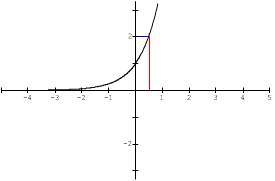
Does this spark some meaning for the expression 
? Carry out the investigation which analyses TABLES OF VALUES to determine the meaning.
In Step A , using the graphing technology, enter each function and copy the TABLE into your notebook (you should have three separate tables). In the TABLE SETUP use 
= ½ not 0.5; in Step B, examine x = ½ for each table and find its corresponding y value. You should notice an interesting pattern and be able to answer the questions given.
For Step C and Step D repeat the procedures of Steps A and B. Again it is important that you use 
not its decimal approximation since the patterns will not as readily emerge if the decimal approximation 0.33 is used.
Complete the investigation and its questions before continuing.
In the investigation, you should have discovered
- a power raised to ½ is equivalent to taking the square root of the base of the power
-
a power raised to a is equivalent to taking the cube root of the base of the power
When the exponent is a negative, the power of a power rule can be used to rearrange the exponent to a positive value. For example, since -a can be written as 
we can simplify 
as follows:
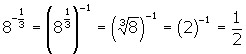
or
What happens when the exponent is an improper fraction such as 
? For example, how can 
be simplified ? From the laws of exponents you know that 
. Using this idea you have
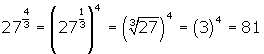
Consider the following examples using rational exponents:
Example 1
Simplify: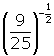 
Solution
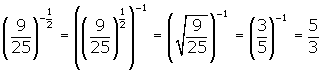
Example 2
Solve for x: 
Solution
Example 3
Solve for x: 
Solution
Example 4
When a painkiller enters the bloodstream, it gradually dilutes, decreasing exponentially with a half-life of 2 hours. If a 100 mg tablet is taken at 4 P.M. at what time will 12.5 mg of the painkiller be still in the bloodstream?
Solution
Let y represent the quantity remaining after x hours.
Initial value (a = 100), half-life (b = ½) is 2 hours (c =2) for .
Activity
Investigation Questions p.164. Complete 1, 2, 3, 4 and 5
Challenge Yourself p.165
Check Your Understanding p.164 - 167. Complete 6 to 21 inclusive
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
After you do the assigned activities, continue on to the Test Yourself section below for a quick quiz on this lesson.
Test Yourself
- Evaluate
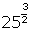and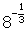 
without using technology and write a Journal entry explaining how you obtain each value. - Solve for x:
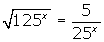
- Using the formula
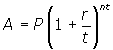( as described in question 18, p.166), answer each of the following questions:
- If you invest $1000 at 4% interest, compounded quarterly, how much money will you have after 2 years?
- To double your money it will take 10 years. What is the nominal rate of interest if compounding is quarterly?
Click here for suggested solutions.