Learning Resources
Lesson
Part I of this Focus recalls for you that certain numbers can be expressed as a power of different bases. A further example would be 16.
- Since 16 = 4 x 4, then you can write
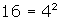; - however, 16 = 2 x 2 x 2 x 2 which means
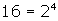. - As well, when you consider that
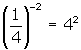, then 
.
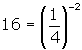The point to all of this is its use in solving exponential equations which is Part 2 of the Focus. If the bases on each side of an exponential equation are the same, then the exponents are equal.
Study the example in the textbook to help you understand how to solve exponential equations.
Remember the key to solving these equations is
- express both sides of the equation as powers of the same base
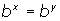if and only it 
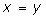(i.e. when the bases are equal, the exponents are equal) provided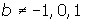 
Example 1
Solve for x : 
Solution:
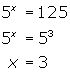
Example 2
If 
,solve for x.
Solution
Use the Go ahead one frame button to view solution:
Example 3
Solve the following equation for x: 
.
Solution
Use the Go forward one frame button to view solution:
Example 4
Solve the equation 
Solution
Before beginning to solve this equation, you should recognize it as a quadratic form. If 
, then this equation could be written as
and then solved by factoring and the zero product property.
Use the Go forward one frame button to view solution:
Activity
Focus Questions p.158 - 159. Complete 8, 9 and 10
Think About p.158, p.161 and p.162
Check Your Understanding p.159 - 162. Complete 11 to 25 inclusive
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
After you do the assigned activities, continue on to the Test Yourself section below for a quick quiz on this lesson.
Test Yourself
- Find the zeros of the function :
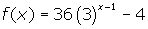
- A cup of coffee contains approximately 100 mg of caffeine. When you drink it, the caffeine is absorbed into the bloodstream and is released by the body exponentially. Every 5 hours the caffeine is reduced by 50%. Write an equation to model this phenomenon and find how long it takes for the the caffeine to be reduced to 25 mg.
Click here to view a suggested solution.