Learning Resources
Lesson
The introduction relates a problem that is very similar to the problem used in the introduction of lesson 01 in Section 01; however, in this investigation you will find exponential functions to describe the number on a given square as well as a function for the total up to and including any given square.
For Step A, copy the table and complete as illustrated for the first 6 to 10 squares - complete enough to find the patterns. Do NOT attempt to find all 64 squares. The second stage, Step B, requires you to write the number of grains of rice on a square as a function of the square. Use only the first two columns of the table and identify the pattern. Don't be hasty but stop and think about the two columns - the second has to be a function of the first.
The function g(x), in Step C, is a little more difficult to find. You are told that it is an exponential function, but there is no common ratio between successive y-values ; this means, if you recall from earlier lessons, it must be of the form 
. Think about what you could add or subtract to the numbers in column 3 to create a set of numbers that will have a common ratio.
Complete the investigation questions before continuing.
If you were not successful in finding the functions in the investigation, consider the functions 
and 
. Check their tables of values either by calculation or technology and compare the tables of values generated to the table in Step A.
As well, in the questions recall the use of function notation. 
means exactly the same as the equation form. For example, f(5) means find the y value when x = 5 . (i.e. 
)
If 
, you are asked to find an x value for the function that will result in a y value of 8. ( i.e. 
) This can be done by using a graph. Step through the following procedure to view a solution.
Alternately, if you recognize that 
, then we could reason as follows:
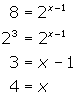
This idea becomes the core of solving certain exponential functions algebraically.
Activity
Investigation Questions p.156 - 157. Complete 1, 2, 3, 4, 5, 6 and 7
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
After you do the assigned activities, continue on to the Test Yourself section below for a quick quiz on this lesson.
Test Yourself
Write a Journal entry explaining why the graphical method of solving exponential equations is not always the best method.