Learning Resources
Lesson
In the exponential function 
, recall that the a represents the starting value or initial value for the data and b is the common ratio for equal increments of x.
In completing this investigation, Step A and Step B should pose no problems. By using the common ratio, the table can easily be expanded and the equation written in the proper form. In Step C and Step D, simple substitution of the time required to double or quadruple into each equation will determine the correct function. However, be sure to explain why the function found makes sense in the context of the data and the situation.
Complete the investigation questions as assigned in the Activities Section.
After completing the investigation questions, you should realize that the base of the exponential function can be controlled by analyzing the tables of values for patterns and appropriately changing the exponent.
Example 1
If a certain strain of bacteria grows according to the following table, find an exponential equation to describe it. Write the exponential equation based on doubling time; on quadrupling time.
Time (min) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
Number of bacteria |
100 |
126 |
159 |
200 |
252 |
317 |
400 |
Solution
The common ratio for equal increments of x can be found by looking at any two consecutive y-values which gives
The initial value is 100. Therefore, for , we have a = 100 and b = 1.26 giving the function
From the table, the doubling time in minutes is 3. For doubling time the common ratio is 2, which means b = 2 with a = 100. We must ensure that the exponent at 3 minutes is 1 to guarantee the number of bacteria to be 200 and the exponent at 6 minutes is 2 to guarantee 400 bacteria. Therefore,
since 
and 
.
Using the same argument for quadrupling, the base is 4; at 6 minutes the exponent has to be 1 giving the function
Note in this process the initial value a does not change but by changing the base the independent variable x has to be operated on to reflect that change. The equation now takes the form 
which means for the above example
- the number of bacteria increases by a factor of 1.26 for every minute
- the number of bacteria increases by a factor of 2 for every three minutes
- the number of bacteria increases by a factor of 4 for every six minutes
In changing the functions in this way, it has an effect on the graph. Graph the basic exponential 
and 
on the same co-ordinate plane. What do you notice? We will return to this in a later lesson !
If you require further examples go to the next page.
Example 2
A bacteria strain triples every 8 minutes. If there are 850 bacteria in the culture initially, write an equation to describe its growth. How many bacteria are in the culture after 12 minutes?
Solution
Initial value (a = 850), triples ( b = 3) every 8 minutes (c = 8) .
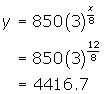
After 12 minutes there are approximately 4416 bacteria in the culture.
Example 3
The half-life of iodine is 4 days. If a sample of 60 grams is used, how much remains after 22 days?
Solution
Initial value (a = 60), half-life (b = ½) is 4 days (c = 4) for .
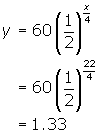
After 22 days 1.33 grams of the iodine remains.
Activity
Investigation Questions p.135 - 136. Complete 26, 27, 28, 29 and 30
Think About p.136
Check Your Understanding p.136 - 138. Complete 31 to 39 inclusive.
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
After you do the assigned activities, continue on to the Test Yourself section below for a quick quiz on this lesson.
Test Yourself
In your Journal explain why or why not that an initial strain of 500 bacteria that doubles in 8 minutes will have 750 bacteria in 4 minutes.
Alcohol in the bloodstream is reduced by half every 3 hours. If there are 
in the bloodstream, write a function to represent this information and find how much remains after 8 hours.
Click here for a solution to the problem.