
Learning Resources
Lesson
Read the introduction to this investigation which gives an example where functions of the form ![]() are applied in the medical profession. To get a better understanding of how such functions work complete the investigation.
are applied in the medical profession. To get a better understanding of how such functions work complete the investigation.
In Step A, you can create six individual tables as below :
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
y |
or create one table for (a) and one for (b) as the one below for (a)
x |
(0.8)x |
4(0.8)x |
2(0.8)x |
-3 |
|||
-2 |
|||
-1 |
|||
0 |
|||
1 |
|||
2 |
|||
3 |
Draw graphs in Step B on your own paper. Refer to the note in the side-bar of your textbook recommending that you use different colours for each graph to help distinguish between the functions on your co-ordinate plane.
Complete the investigation questions to find the characteristics of these type functions. For hints and suggestions, go to the next page.
As a further example to the investigation questions, consider the graphs of ![]() and
and ![]() as pictured below:
as pictured below:
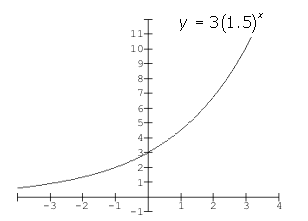
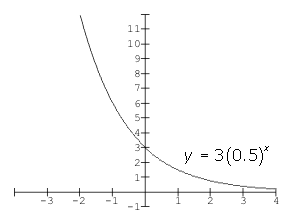
From these graphs we can see that
- the focal point is
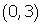 or in the form
or in the form 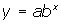 it would be the point
it would be the point 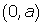 which is the y-intercept.
which is the y-intercept. - when the b > 0 as in
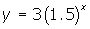 , the curve is increasing from left to right and is a growth curve
, the curve is increasing from left to right and is a growth curve - when the b < 0 as in
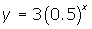 , the curve is decreasing left to right and is a decay curve
, the curve is decreasing left to right and is a decay curve - For both functions, there is no x-intercept but if the graphs are extended far enough to the left for
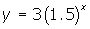 and to the right for
and to the right for 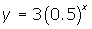 , the curves will come extremely close to the x-axis; in fact we can get as close to the x-axis as we want by choosing a big or small enough value for x. The x-axis or its equation y = 0 is called an asymptote for the curve.
, the curves will come extremely close to the x-axis; in fact we can get as close to the x-axis as we want by choosing a big or small enough value for x. The x-axis or its equation y = 0 is called an asymptote for the curve. - If we compare these graphs to
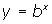 , we note that the 3 is a vertical stretch of
, we note that the 3 is a vertical stretch of 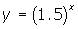 or
or 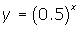 . For
. For 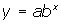 , the form
, the form 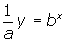 is its transformational form with a vertical stretch of a .
is its transformational form with a vertical stretch of a .
Example
What can you say about the values of a and b for the graph below:
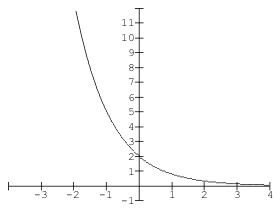
Solution
This is an exponential function based on its shape. The a value would be 2 since it is the y-intercept of the graph and b < 0 since it is a decay curve. The asymptote is the x-axis or the line with equation y = 0 .
Activity
Investigation Questions p.128. Complete 1 to 8 inclusive
Think About p.128, p.129 (2 items) and p.130
Check Your Understanding p.129 -130. Complete 9, 10, 11 and 12
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
After you do the assigned activities, continue on to the Test Yourself section below for a quick quiz on this lesson.
Test Yourself
Write a Journal entry explaining why the exponential curve does not accurately model the medication in the bloodstream with respect to time.
Give an example of an exponential function that
- passes through (0, 3.5) and displays growth
- passes through (0, 4) and displays decay
- compare your graphs with those of your classmates and determine which is growing or decaying fastest.
Click here for exponential function examples.