Learning Resources
Lesson
Investigation 2
In this investigation, you will investigate a new function where the independent variable is an exponent. For example, 
.This type of function is referred to as an exponential function. To crate a table of values of these function, recall the idea of exponents:
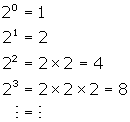
Therefore, a table of values for would be
x |
0 |
1 |
2 |
3 |
y |
1 |
2 |
4 |
8 |
The purpose of this investigation is to discover if there is a common ratio between successive y-values for equal increments of x ( i.e. the difference between successive x-values is constant).
Materials required for this investigation include
- graph paper
- graphing technology
It's a good idea to work with a partner, if possible, while working on this investigation. After attempting the work together, if there are problems go to the next page for hints and comments.
Complete the investigation and investigation questions before continuing.
Steps A through E should be very straightforward and pose no serious problems ! Be sure to draw these graphs on graph paper as instructed without using technology. Save these in your notebook to refer to later.
Step F is important since it will confirm or deny the relationship regarding common ratios between the successive y-values.
In the investigation questions, the tangents to the curve have to drawn and their slopes found to determine whether the curves are increasing or decreasing. This can be done using the TI-83. Click here to see a demonstration of how to perform this operation if you do not already know how to find the tangent and its equation.
After completing this investigation you should be able to associate the curve drawn with rates of growth or decay.
Continue on to the Focus on the next page when you have this activity completed.
Focus B
Exponential functions are very powerful since they can be used to model many real-world relationships as pointed out in your textbook.
is the simplest exponential function where b is the base, x is the exponent and bx is referred to as the power. These functions have the point 
in common since for x = 0 the value of b0is always 1.
To find y-values for given x values it is a simple matter of using the calculator and raising the base to the appropriate exponent. For example, find y if x = 9 in the equation .
However, if the y-value is given, it is more difficult to find the x value. For example, find x if y = 48 in the function . This means we have to solve an equation that looks like this:
. This can be solved by entering the function into your calculator and using the TBLSET and TABLE to find an approximate value. To view a solution for this type of equation click here.
To determine if a set of data can be modeled by a linear, quadratic or higher power function we can use a sequence of differences as seen in unit 1. If a set of data has a ratio of successive y-values that is constant for equal increments of the x-values, then the data can be represented by an exponential function.
Complete the Focus questions on p.116 as assigned in the activities.
Activity
Investigation Questions p.115. Complete 15 to 21 inclusive
Challenge Yourself p.114 and p.117
Think About p.116 ( 2 items) and p.118
Focus Questions p.116. Complete 22 to 28 inclusive
Check Your Understanding p.116 - p.119. Complete 29 to 33 inclusive
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
After you do the assigned activities, continue on to the Test Yourself section below for a quick quiz on this lesson.
Test Yourself
Write a Journal entry describing some interesting features of the exponential function in the form .