Learning Resources
Home » » Courses » Mathematics » Advanced Mathematics 3205 (delisted) » Unit 02 » Set 03 ILO 01 » Go to Work
Lesson
The following hints and suggestions are offered to help you progress through these case studies and successfully complete each.
Case Study 1: Charity Fundraiser
- The function can be found by using quadratic regression and/or a system of equations.
- Using graphing technology, graph the function and interpret the rates of change from the graph as required.
- Profit is found by multiplying the number of rolls sold by the profit per roll. Of course, for each roll the profit is the difference between the selling price and the cost.
- Read instantaneous rates of change from the graph and/or calculate by using the slope formula for secants very close to the point to determine the slope of the tangent line.
Case Study 2: Population Change
- Read from the table where the population is increasing (+) no change (0), and decreasing (-).
- Create linear functions using two points in the point slope form of the equation
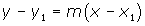and describe what a linear rate of change means. - Find the quadratic equation by using regression analysis and/or a system of equations.
- Read instantaneous rates of change from the graph and/or calculate by using the slope formula for secants very close to the point to determine the slope of the tangent line.
Extension: Rate of Change
Refer to question 29, section 2.2 , page 94 for the set-up for this extension. Obtain a copy of its solution found in the Teacher Resource Book from your in school teacher.
The formula for the volume of a sphere is 
. In fact the change in volume as a function of the change in radius is 
, the surface area of the sphere.
Activity
These items may be used by your teacher as items for:
- a portfolio item
- as a homework project as part of an end of chapter review
- as a quiz item or test item
Test Yourself
Discuss issues surrounding these case studies/extension with your teacher and on/or classmates.