Learning Resources
Lesson
In this lesson continue with your project folder and completely answer the questions posed. Your teacher may request this project to be submitted all or in part at any time. The following hints and suggestions may help you to complete the project and if you require further help contact your teacher or fellow students.
When x% of the circle is removed, then the part that remains (100 - x)% forms the circumference of the base of the cone. Since the radius of a circle is proportional to the radius ( i.e.
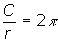) , then the radius can be expressed as 
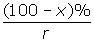. Using this idea, you should be able to justify why the given expression can be used for the radius. The slant height of the cone is equal to the radius of the original circle. Why? Use this to justify the length of the hypotenuse.Justify the given expressions for each side of the triangle and use the Pythagorean relationship to write h and a function in terms of x.
-
Recall the volume of a cone is found by using the formula
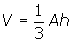where A represents the area of the base. The given expression can be deduced using this formula. -
Replace the h in the formula with its function obtaining the required function for Volume in terms of x. Use technology to graph the function.
-
Note that the Volume will be a maximum at the point where the slope of the tangent is zero. Interpret the changes in slope of the tangents in terms of increasing and decreasing volumes.
Activity
Answer the questions on p.96
Test Yourself
No test items in this lesson; however, be prepared to discuss the water cooler cups project with your teacher and/or your fellow students.