Learning Resources
Lesson
Before beginning this investigation recall that the average rate of change was described as the ratio of difference in the distance traveled to the difference in time traveling as given below:
From previous work in mathematics you know that the slope of a line is given as follows:
You should note the obvious similarity ! The average rate of change between two points is the same as the slope between those two points. This idea is used extensively in this investigation.
Read and study the introduction to the investigation making note of the extensive table of values. This table breaks down the distance versus time over three minutes, divided into 5 second intervals.
- time zero is 12:43:00
- time 60 is 12:44:00
- time 120 is 12:45:00
- time 180 is 12:46:00
- time 240 is 12:47:00
- time 300 is 12:48:00.
- To look at this in reverse 12:46:35 would be time 210 in the table.
The purpose of this investigation is to observe the relationship between the slope of a tangent to a curve at a point and the rate of change of the curve at that point. To complete this investigation you will require
graph paper and/or graphing technology
Complete the investigation and the investigation questions before continuing. beyond this point. You should focus on the graph and the lines you are asked to construct rather than just the table of values to achieve the visual effect of this investigation. If you are having problems or difficulties, go to the next page before approaching your teacher.
Step A
It is recommended that you use technology to graph this material. Using the TI-83 graphing calculator, you can input the times into L1 and the distances into L2 and use a STAT plot to plot L1 against L2. Once this is complete you will have a graph that resembles this
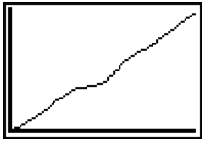
Copy this into your notebooks on a larger scale if possible. Answer the question whether the graph is discrete or continuous.
Step B
A secant to a curve is a line that intersects a curve at more than one point. These two points can be joined on the TI-83. Change the WINDOW settings to Xmin = 60 and Xmax = 240 to draw the secant connecting (60,1276) and (240,5144). You can use the DRAW menu to connect the endpoints of the curve within this window. This results as follows:
To find the slope either try to find it from the graph or use the slope formula.
Step C
Repeat the procedure above for the two given pairs of times !
Step D
This is the crucial step in the investigation. Look at the graphs you have from Steps B and C. The secant lines should tell you something as well as the slopes of these secant lines which should lead you to the conclusion regarding the tangent line at (150,2757). Remember these slopes are essential the rate of change or speed of Mr. Liam for these time intervals. What does the slope of the tangent at (150,2757) represent in this context?
Step E
Repeat the process as above for the given time periods to decide if Mr. Liam was indeed speeding at 12:46:00.
Since the tangent to a curve at a point is a line that intersects a curve at a point and has the same slope as the curve at that point, this becomes the instantaneous rate of change for a moment in time.
Generalizing this idea, if we considered a point on the graph of a function as 
and choose points that are h units away for very small values of h , the slope of the tangent line can be approximated as
(i.e. using two points on either side of which are very close (the closer the better) to we can approximate the slope of the tangent at that point and as a result of the rate of change at that point)
Activity
Investigation Questions p. 86. Complete 1, 2, 3, 4, 5 and 6
Challenge Yourself p.85
Think About p.86
Check Your Understanding p.86 - 87. Complete 7 and 8
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
After you do the assigned activities, continue on to the Test Yourself section below for a quick quiz on this lesson.
Test Yourself
Write a Journal entry explaining in your own terms what you understand by the phrase instantaneous rate of change and how you would find it by using tables and graphs.
- Using the graph and/or the table from the investigation find
- the average speed between 12:44:00 and 12:45:00
- the average speed between 12:44:15 and 12:44:45
- the average speed between 12:44:25 and 12:44:35
- the estimated speed at 12:44:30
Click here for a sample solution.