Learning Resources
Lesson
Recall that when discussing the graphs of linear functions, the slope of the line indicated a number of characteristics as follows:
- lines with positive slope slants upward from left to right
- lines with negative slope slants downward from left to right
- lines with zero slope were horizontal
- vertical lines have no slope
- the steeper the line the greater the slope of the line
Keep these in mind as you complete Focus A. You can work on your own or work with a partner for this activity; If you experience difficulty, go to the next page for hints and suggestions.
Complete the Focus questions (p.79). Make note of the notation used in number question 10.
Go to activities section after completing this focus !
Step A
The graph for the information from Investigation 1 should look like this
Step B
To find the rate for these given times use the points (0,0) and (50,80) for the first 50 minutes and for the last 70 minutes use the points (80,110) and (10,15) then the average rate can be found by finding the ratio of the change in the distance to the change in time. This can be symbolized as
Step C
What do you notice about the graph for the first 40 minutes? Is the rate and the slope the same for this time period? Explain.
Step D and E
Think about the "steepness" of the line segments and what it represents. You can discover when the speed (i.e. rate ) changed either by calculation or examining the steepness of the curve between points.
Step F
First convert 30 km/h to km/min since the graph is in km/min. Find segments on the graph where the slope is that number of km/min to find the correct answer.
Step G
Use the finite differences for the kilometres traveled to determine which type of power function this would represent and with regression analysis find the equation OR use three points to create a system of equations from the quadratic 
, then check to determine if the fourth point satisfies the equation found.
To complete the questions relating to 105 minutes extend the above graph in Step A with the new information and find the solution using the graph.
Go to activities section after completing this focus !
Activity
Focus Questions p.79. Complete 7, 8, 9, 10, 11 and 12
Think About p.78( three items ), p.79, p.81 and p.83
Challenge Yourself p.83
Check Your Understanding p.79 - 83. Complete 13 to 25 inclusive; click here for a reference for question 14
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
After you do the assigned activities, continue on to the Test Yourself section below for a quick quiz on this lesson.
Test Yourself
- A ball thrown into the air with a velocity of 22 m/sec is h meters above the ground after t seconds where
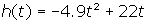. Use function notation to describe the rate of change in height
- between 0 seconds and 2.2 seconds
- between 2.2 seconds and 4.5 seconds
- How do you interpret these results?
- The table below shows the number of people in the age range 15 to 24 years in Canada during various census years
- What would the calculation
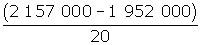tell you about population change in Canada? - During what ten year period shown in the table did the percent of the population that is 15 to 24 years old grow the most?
- Would you expect the population of Canada to grow at the same rate as the number of people aged 15 to 24 years? Explain why or why not.
- What would the calculation
Census year |
Number of people age 15 -24 |
Total Canadian population |
1931 |
1 952 000 |
10 377 000 |
1941 |
2 152 000 |
11 507 000 |
1951 |
2 157 000 |
14 010 000 |
1961 |
2 617 000 |
18 238 000 |
1971 |
4 004 000 |
21 568 000 |
1981 |
4 659 000 |
24 568 000 |
1991 |
3 831 000 |
27 297 000 |
For sample solutions , click here