Learning Resources
Lesson
Read the intro to Investigation 5 and complete the procedures as outlined in your text book (p.48 - 49). For help with the procedure read the steps below.
Step A
If the house numbers differ by 2, then if n represents the first house number
(n + 2) or (n - 2) will represent the second house number . Now set up your quadratic equation to model the given problem.
Step B
Using the values for a, b and c from your equation, solve the quadratic equation by substituting these values into the quadratic formula that is given in your text book. Make sure to simplify your answer as much as possible.
Step C
You should use completing the square to verify your roots since you will need to review this process for the questions that follow.
Step D
This is an important step since roots or solutions to equations must be interpreted in terms of the problem or they have no meaning.
Complete the Investigation Questions before continuing with this lesson!
You have used completing the square procedure for
- changing the general form of the quadratic equation to the transformational form
- locating the x-intercepts ( when y = 0 ) for the graph of a quadratic function
- finding the roots of a quadratic equation
The steps to complete the square of a trinomial expression with 
should be quite familiar to you. With your experience using this techniques, you should be able to solve 
with as a general statement. Try It !
You might want to solve 
by completing the square and justify each step and at the same time solve and justify each adjacent step. When you have completed this you will have successfully derived the quadratic formula.
After completing this exercise click here to compare your solution to the recommended solution.
Go to the next page for an example of using the quadratic formula to solve quadratic models.
Example
Solve the following quadratic equation: 
Solution
To use the quadratic formula we note that 
; substitute these values into the formula:
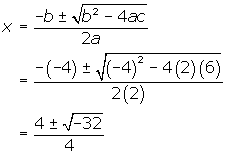
You will note that the square root of a negative number occurs in this solution which means that the roots are complex since 
is an imaginary number. Recall that it simplifies as follows:
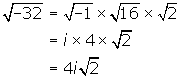
Therefore, the solution to this equation will be
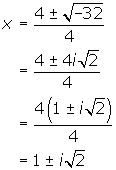
The solution to the equation is 
.
Activity
Investigation Questions p.48. Complete 23 to 29 inclusive
Check Your Understanding p.49 - 50. Complete 30, 31, 32 and 33
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
After you do the assigned activities, continue on to the Test Yourself section below for a quick quiz on this lesson.
Test Yourself
Solve the following equation ( note any restrictions on this equation ) : 