Learning Resources
Lesson
As evidenced in lesson 1, converting between the various forms of the quadratic requires many algebra skills. From that lesson you can now convert transformational form to standard form to general form. It is also necessary to work in the opposite direction since the transformational form has some advantages in terms of reading characteristics of the parabola directly from the equation.
Example 1
Change 
into transformational form.
Solution
Follow the steps by clicking on the Go forward one frame button below and navigate the window by using the Global action buttons. Read and follow each step:
From the above example you can see with very little algebraic manipulation the transformational form can be found from the standard form.
Now, to convert from the general form to the standard form, requires the rearranging of elements to find a perfect square trinomial. Study the Focus example which relates "completing the square" to the use of algebra tiles. You should get a set of tiles and model this process.
Complete all Focus Questions before continuing with the lesson.
After completing the focus questions, you should have discovered the relationship between the coefficient b and the constant added to complete the square when a = 1 . Consider the following example to support your findings:
Example 2
Create the transformational form for the equation 
.
Solution
Follow the steps by clicking on the Go forward one frame button below and navigate the window by using the Global action buttons. Read and follow each step:
Note: To complete the square for 
take 
of 4 and square it; add to both sides of the equation to keep it balanced and simplify by factoring.
In general, to complete the square for 
, multiply b by and add its square to to obtain 
As you discovered in the focus questions if the a in the equation is not 1 then it must be removed before completing the square.
Example 3
Find the transformational form for the equation 
Solution
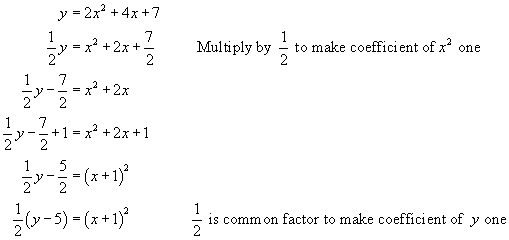
The obvious advantage to this form is that the vertex, the axis or line of symmetry, the vertical stretch and maximum or minimum value of y can be read directly from the equation.
Activity
Focus Questions p.32 - 33. Complete 14 to 22 inclusive
Think About p.32
Challenge Yourself p.33 and p.35
Check Your Understanding p.34 - 35. Complete 23 to 34 inclusive
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
After you do the assigned activities, continue on to the Test Yourself section below for a quick quiz on this lesson.
Test Yourself
Write a journal entry explaining step by step how to change 
to transformational form.
Write a solution for the following problem
The hammer throw is a very competitive event in the Summer Olympics. If 
models the height h reached by the hammer after t seconds of flight for one of the competitors, what is the maximum height reached by the hammer?
Sample solution, click here.