Learning Resources
Lesson
In this lesson you will use the common differences in a quadratic sequence and systems of equation to find the equation that generated the sequence.
Example
Find the equation that generated the sequence {-4, 5, 18, 35, 56}
Solution
First find the second-level differences:
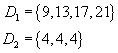
Since we know that the common difference is twice the value of a in the equation 
, we have
Therefore, the equation takes the form 
. Now substitute any two of the terms from the sequence into the equation to obtain a system containing b and c . Use the first and second terms.
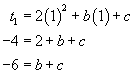
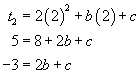
From the first term expression 
; from the second term expression 
. Therefore, by substitution we find
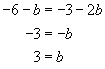
Substituting we find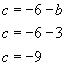 
The required equation is 
(Note: For those who have completed Math 2205, you may use any of the methods learned to solve systems including substitution, elimination or matrices)
Activity
Focus questions p.12. Complete 34, 35, 36 and 37
Challenge Yourself p.12 and p.13
Check Your Understanding p.12-14. Compete 38 to 42 inclusive
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
After you do the assigned activities, continue on to the Test Yourself section below for a quick quiz on this lesson.
Test Yourself
Find a cubic equation to describe the sequence {-1, 0, 9, 38, 99} (Recall the use of matrices to solve systems of equations )
Check Your Answer.