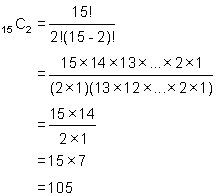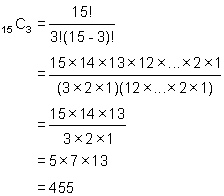Learning Resources

Investigation 14: Pascal's Triangle and the Expansion of (x + 1)n 

Test yourself (Answers)

The coefficients of the first four terms of the expanded version of (x + 1)¹⁵  are the first four elements of row 15 of Pascal's Triangle.

The first element of any row of Pascal's Triangle is always 1 and the second element is always the row number. Thus the first coefficient is 1 and the second coefficient is 15.

From our previous work on the relation between Pascal's Triangle and combinations, we know that the first four elements in row 15 are ₁₅C₀ , ₁₅C₁ , ₁₅C₂ , ₁₅C₃ . As noted in the paragraph above, we know what ₁₅C₀ and ₁₅C₁ work out to be (you can double check if you like by working out their value using the formula for combinations).

All we have to do is calculate ₁₅C₂ and ₁₅C₃ :

Thus the first four terms of the expansion are:

(x + 1)¹⁵ = x¹⁵ +15x¹⁴ + 105x¹³ + 455x¹² + .....