
Learning Resources
Lesson
Before we consider how to count/calculate the number of permutations on a given set, we have to consider a new notation that will be of immense benefit in these calculations. This new notation is introduced by means of the following example.
Example
Suppose there are 10 people in your Mathematics 3204 class who write a unit test. Also, suppose each receives a different score on the test. In how many different ways could the 10 scores have been distributed among the 10 students?
Solution
From our work on Investigation 10 in the last lesson we can reason as follows. There are 10 different people who could have received the highest mark. That leaves 9 different people who could have received the second highest mark. Similarly, there are 8 who could receive the third highest mark, and so on.
By the Fundamental Counting Principle, the total number of ways the 10 marks could have been distributed to the 10 people are:
10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1
This is a very large number (3 628 800 to be exact). In fact, the product of successive integers starting at a certain integer and continuing down to 1 gets unwieldy very quickly (try 15 x 14 x 13 x ....x 3 x 2 x 1 and you will see for yourself).
To write such an expression every time we have to deal with a similar type of problem would be a pain. However, mathematicians have solved that problem for us. They invented a notation that would represent that product without actually writing it all out. To express the first product above, 10 X 9 X ...X 2 x 1, we simply have to write 10!. Similarly, to express 15 X 14 X 13 X ...X 2 x 1, we write 15!.
The "!" symbol is not read as in English. In mathematics, we do not say "10 exclamation mark". In mathematics we read it as "10 factorial".
Factorial: The product of all positive integers equal to and less than a given
positive integer. The notation for it is n!, and this is read as "n
factorial". Thus:
n! = n x (n - 1) x (n - 2) x (n - 3) x ... x 3 x 2 x 1
This notation will be very beneficial in the rest of our work on permutations and combinations. Some examples of its use are shown below:
Example 1
Example 2
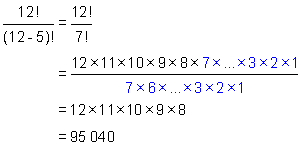
Example 3
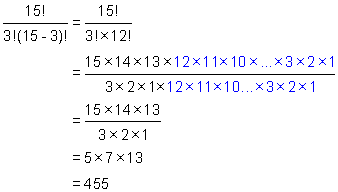
We now have to see how this notation occurs in our attempt to count or calculate permutations.
As we have said many times, calculating probability is a matter of counting the total number of possible outcomes and the number of ways out of this total that event X can occur. In a later lesson we will use the number of permutations to help calculate the probabilities of certain events. In this lesson we will concentrate only on how to count permutations.
First lets look at Example 1 from the previous page again:
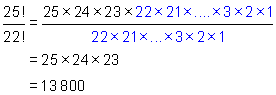
Think about working backward in this problem. If we are given the product
25 x 24 x 23 can you see how to write it as the quotient of two factorials?
How could we write 14 x 13 x 12 x 11 as a quotient of factorials? Note that the product is the first part of the expansion of 14! since:
14! = 14 x 13 x 12 x 11 x 10 x 9 x 8 x... x 3 x 2 x 1
The part we wish to eliminate by division is 10!. Thus we have:
![]()
Let's see how this can be applied to counting permutations by reconsidering a version of the problem considered on the previous page:
Example
Suppose there are 10 people in your Mathematics 3204 class who write a unit test. Also, suppose each receives a different score on the test. In how many different ways could the 1st, 2nd, and 3rd highest scores have been distributed among the 10 students?
Solution
Since order matters in this problem, what we are counting is the number of permutations of 10 objects taken 3 at a time. There are 10 students, thus 10 ways of assigning the 1st mark, 9 ways of assigning the 2nd mark, and 8 ways of assigning the 3rd mark. By the Fundamental Counting Principle this means there were 10 x 9 x 8 different ways of assigning the mark.
We now wish to express the product 10 x 9 x 8 as the ratio of factorials. This gives:
![]()
The numerator of the fraction is obviously the number in the sample set, viz. the 10 students in the class. But what about the denominator? What is its relation to the numbers in the original problem?
Recall there were 10 in the sample set (the number of students) and we were assigning 3 marks in order. Note that 10 - 3 = 7. We could thus write the above expression as:
![]()
Thus we can say that the number of permutations of 10 items taken 3 at a time is given by the formula:
![]()
It is cumbersome to write "the number of permutations of 10 items taken 3 at a time". Once again mathematics has provided a shorthand way of writing this English expression. The notation used for the above expression is 10P3 and we read this as "10 permute 3".
Some examples of applying this formula and the notation are shown below:![]() "the number of permutations of 20 items taken 5 at a time"
"the number of permutations of 20 items taken 5 at a time"
![]() "the number of permutations of 15 items taken 10 at a time"
"the number of permutations of 15 items taken 10 at a time"
Formula for Calculating Permutations
In general, we can say that "the number of permutations of n items taken r at a time" or "n permute r" is given by the formula:
![]()
You should now be ready to do the work assigned for this lesson.
Activity
- Read through Examples 4, 5 and 6 in Focus F on pages 329 & 330 in your text.
- Do the CYU Questions 8, 9, 11 - 13 on pages 330 & 331.
- Complete Investigation 11 on page 331 (this is similar to the work done in the lesson and you may omit it if you understand the derivation of nPr).
- Complete the Investigation Question 15 on page 331.
- Do the CYU Questions 16 - 20 on page 332.
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
- In horse racing, the exactor is betting on which horse will finish 1st, which one will finish 2nd, and which one will finish 3rd. In a race with 9 horses, how many different ways are there for picking the exactor?
- How many different 4 letter permutations can be made from the word DEMOGRAPHY?