Learning Resources

Lesson

We said in an earlier lesson that to calculate theoretical probability we have to count two things: the total number of possible outcomes and the number of ways a given event X can occur. This lesson deals with how to count the number of permutations and combinations of a given set of objects.

Let's begin by first defining what each of the terms mean. Then we will then turn our attention to counting them.

Permutation: A permutation is an arrangement of a set of things in a particular order.

Suppose the set is the letters P, Q , R. If we consider all three elements of the set, the permutations are: PQR, PRQ, RPQ, RQP, QPR, QRP. The order of the letters matter. Each arrangement is a different permutation of the original set. There are 6 different permutations in all.

We could also select only 2 of the 3 elements from the set P, Q, R and consider the different permutations of these. The different permutations of two elements from this set would be: PQ, QP, PR, RP, RQ, QR. Again order matters. Each arrangement is a different permutation of 2 elements of the 3 in the set. There are 6 different permutations in all.

Combination: A combination is an arrangement of a set of things without regard to order.

Consider the second situation above: select 2 of the 3 elements of the set P, Q, R and determine the different combinations of these. Since a combination does not regard order, the arrangements PQ and QP are the same combination. Similarly PR and RP are the same combination, and RQ and QR are the same combination. There are only 3 different combinations of 2 things taken from a set of 3.

Investigation 10 on page 327 in your text deals with permutations and combinations. If you have difficulty with it, some hints and directions are given below.

Investigation 10

Step A

This step deals with combinations. You should check with your classmates (either on site or via the net) to ensure that you have all the required combinations before you go on to Step B. (Hint: you should have 10 of them). Be systematic in the way you make your listing and you should obtain all of them.

Step B

This step involves permutations. There is a lot more arrangements here than in Step A. Organize you work to have a systematic approach to the listing and share the work with a classmate. For example, you could list all the permutations involving A and your classmates permutations that don't involve A.

Hint: Instead of listing all the possibilities , can you count them without listing? How many ways can the highest mark be assigned? Once the highest mark has been assigned, how many ways are left to assign the second highest mark? The third highest? Could a tree diagram diagram and the Fundamental Counting Principle help? A partial tree is constructed below to show you the possibility:

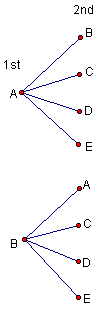
There are 5 people to whom you can assign the highest mark ( A, B, C, D, or E). Once the highest mark has been assigned there are only 4 people left to whom you can assign the second highest mark (this is shown in the tree diagram above).

Step C

Make sure to record in your notebooks the response to this question. It is answered on the first page of this lesson. You need to record it for future reference.

Activity

1. Complete Investigation 10 on page 327 in your text.
2. Complete the Investigation Questions 1 & 2 on page 328.
3. Do the CYU Questions 3 - 7 on pages 328 & 329.

When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.

Test Yourself

Identify each of the following as an example of a permutation or a combination.

1. Picking two names from a hat to receive a prize of $50 each.
2. Picking two names from a hat, the first to receive a prize of $50 and the second a prize of $25.
3. Picking six numbers for the Loto 649 draw.
4. Picking which three horses will be leading at the end of an 8 horse race.
5. Picking which horse will finish first, which horse will finish second, and which horse will finish third in an 8 horse race.

Solution