
Learning Resources
Lesson
In the previous lesson we discussed mutually exclusive events. We saw that if event A was mutually exclusive from event B, then:
![]()
However, if the events A and B were not mutually exclusive, then the above relation/formula did not apply.
What we wish to do in this lesson is to determine a formula for finding
P(A OR B) when the events are not mutually exclusive. The demonstration below shows a Venn Diagram for two non-mutually exclusive events A and B, and provides a justification for the formula for P(A OR B).
Remember the formula P(A OR B) = P(A) + P(B) - P(A AND B) was derived based on non-mutually exclusive events. However, if the events are mutually exclusive, then P(A AND B) = 0 and the formula reduces to the one shown at the beginning of this lesson.
Although it is nice to know how the formula for finding P(A OR B) for non-mutually exclusive events can be justified or proven, that is not the main outcome of this lesson. Our main outcome is to be able to identify when events are not mutually exclusive and use the above formula to calculate P(A OR B).
Example
In a survey of 120 high school students it was found that 60 had a part time job, 40 were involved in clubs or other activities outside school, and 20 had both a job and were involved in clubs or other activities outside school. What is the probability that a student selected at random from the 120 has a job or is involved in clubs or other activities outside school.
Solution
Let event A be "have a part time job" and event B be "involved in clubs". Then:
![]()
![]()
![]()
Since the events are not mutually exclusive (some students are in both sets), we can use the formula developed on the previous page:
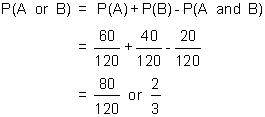
We can also represent the same problem using a Venn Diagram as shown below:
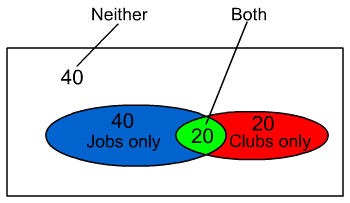
From the diagram we have:
![]()
Now go to the top of the page and click on the Activities button. However, before you do, please note that there is an error in your text book on page 314. The book gives:
![]()
It should be:
![]()
Activity
- Read through Focus C on page 314 in your text.
- Complete the Focus Questions 30 & 31 on page 314.
- Do the CYU Questions 32 - 36 on pages 314 & 315.
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
The probability of having snow on the May 24th. weekend is estimated to be 45%. The probability of having snow on the November 11th. weekend is estimated to be 60%. The probability of having snow on both weekends is 15%. What is the probability of having snow on at least one of these weekends?