
Learning Resources
Lesson
This lesson continues the work on experimental probability and how to use simulations to determine them. Open your text to page 304 and read through Investigation 2. The investigation deals with the probability of two people meeting each other under certain conditions. Since there are two people/events involved your simulation must involve two separate trials one for each person.
You need to set up a simulation that will select a time for Alyssa between 10:00 and 10:30 and also select a time for Ja-Wen between 10:00 and 10:30. If the two times are 10 min or less apart they meet. If the two times are greater than 10 min apart they do not meet. Some suggestions of how you might set up the simulation are shown below.
Suggestion 1
One simple simulation would be to use two bags (boxes, hats, etc.), one for each person. In each bag put pieces of paper with the times on it, e.g. 10:00, 10:01, 10:02, .....,10:29, 10:30. Draw one piece of paper from each bag and record the results in a table similar to the one on page 305 of your text. Compare the two times and decide if they meet. Replace the pieces of paper, shake the bag, and repeat the process 50 times.
Suggestion 2
You could also use your TI83 calculator to simulate this problem. Use it as you did in the examples in the previous lesson. This time you want to select 2 random integers between 0 (representing 10:00) and 30 (representing10:30). If the difference between the two random integers is 10 or less, the people meet, otherwise they don't. One result of this is shown below:
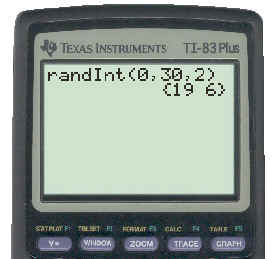
In the trial above, we interpret the simulation result (19 , 6) as meaning Alyssa arrived at 10:19 and Ja-Wen arrived at 10:06. That means they did not meet each other. Use your calculator to repeat this 50 times and record your results in a table similar to the one on page 305 in your text. To see the key strokes necessary to perform this simulation click here.
Suggestion 3
If you use the TI83 as described above, you will have to repeat the process 50 times. One way of getting around this is to pick the 50 random numbers representing the 50 possibilities for Alyssa's arrival time and store them in a list. Then do the same for Ja-Wen's arrival times. Compare the corresponding numbers in the lists to see if they "meet". One result is shown below:

The first pair (18 , 24) indicate they will meet as the difference is less than 10. The third pair (6 , 18) indicate they will not meet as the difference is greater than 10. To see the key strokes necessary to perform this simulation click here.
Suggestion 4
If you are familiar with the use of spreadsheets such as Microsoft Excel, you can use them to very quickly generate a series of random numbers to simulate this problem.
Caution: The random number generator in Excel works differently than in the TI83. In Excel the function returns a decimal quantity between 0 and 1. To turn the result into integers you have to multiply by the upper limit of the integers you wish to choose and then round the decimal quantity to the integer below it.
A spreadsheet can do much more than simply generate a series of random numbers. In our problem, it can also be "programmed" to tell if the results of a trial mean they meet or not. It can also count the number of times the meeting occurs, and it can return the probability by dividing the number of successful trials by the total number of trials.
The following spreadsheet is set up to do 50 trials each time the simulation is run. By changing the number of the simulation in cell C1, the spreadsheet re-calculates 50 pairs of random numbers, checks to see if they differ by 10, counts the number of "yes" responses, and calculates the probability. You have to scroll down to row 52 to see the answer. You can use the results to help answer Step G in Investigation 1 on page 305. Enter a different simulation number and see how the probability changes.
You should now be ready to do the work in your textbook related to using simulations to find experimental probability.
You should have access to the TI83 calculator and that may be the best method to use for simulation as most events can be modeled using some form of random numbers. If you are comfortable with, and have access to spreadsheets, you have a fast and convenient way of doing many repetitions of the same simulation and/or doing many trials in each simulation. Without one of these pieces of technology, you have to rely on selecting objects (pieces of paper, marbles, etc.) from bags or hats, or tossing dice of some kind.
For example, in exercise 14 on page 305 you could use your TI83 to generate random numbers from 1 to 20 to represent the arrival of Route 3 bus and random numbers 1 to 15 to represent the arrival of Route 5 bus. Since Andrew wants to wait for no more that 5 min, you could let the numbers 1 to 5 represent the arrival of the bus and the other numbers to represent the non-arrival. Record your results in a table similar to the one use for Investigation 2. Tally a "yes" if either bus arrives.
Activity
- Complete Investigation 2 on pages 304 & 305 in your text.
- Do the CYU Questions 14 - 16 on pages 305 & 306.
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
Based on past experience, the probability that Jim will pass his next math test is 50% and the probability that Anne will pass is 80%. Set up a simulation to determine the experimental probability that they will both pass the next test.