Learning Resources

Lesson

We are again going to consider the transformation of the unit circle which has equation x² + y² = 1. In the last lesson, the stretch in both the horizontal and vertical direction was the same, thus preserving the circular shape. In this lesson, we will explore stretching by a different factor in the two directions. The figure thus obtained is called an ellipse. The diagrams below show ellipses formed by this type of transformation.

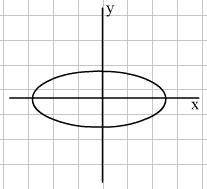
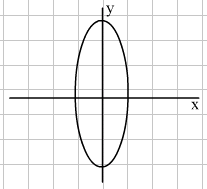
Greater horizontal stretch Greater vertical stretch

The rules for the transformational form are still the same. Multiplying the x value by a factor stretches horizontally, multiplying the y value by a factor stretches vertically. Click any of the buttons below to see the transformation corresponding to the equation. Record in your note books the equation and draw a sketch of it for future reference. Pay particular attention to the size and direction of the stretch and the coefficients of the variables.

The figure produce by stretching a circle by different factors horizontally and vertically is called an ellipse. An ellipse does not have a diameter since its width varies with the direction. It does have two axes: a major axis and a minor axis, the length of which are determined by the stretch factor. The major axis is the longer axis and the minor axis is the shorter one. This is indicated in the diagram below:

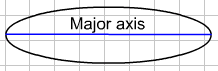
Go back to the transformations above and for each of them record in you note book, next to the equations and graphs you have already sketched, the length of the major and minor axes and then compare them to the coefficients of the variables. Make a conjecture about the relationship between the length of the axes and the coefficients of the squared terms? Click here to see if your conjecture is correct.

Using the major and minor axes is a quick way to sketch the graph of an ellipse. If you draw these axes first, it provides a framework on which to sketch the graph.

The point of intersection of the major and minor axes is the centre of the ellipse:

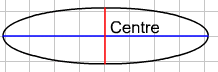
In all the transformations shown above, only a stretch was involved. The unit circle was not translated before the stretch and hence the centre of the ellipse remained at the origin. If a translation is also involved, you can either translate first and then do the stretch, or do the stretch first and then translate.

Example:

Sketch the graph of

Solution

The centre of the ellipse is at ( 3 , -1 ) with a horizontal stretch of 3 and a vertical stretch of 5. The length of the minor axis is 6 and the length of the major axis is 10. The method used is to first translate the unit circle in order to locate the new centre of the ellipse. The stretch is then applied to the diameter by drawing the major and minor axes. And finally, the ellipse is sketched around these axes. This process is shown in the following illustration:

If the equation of the ellipse is in transformational form, it is relatively easy to sketch its graph using the above method. However, most often the equation is not in transformational form and so it has to be rearranged first before this method can be used. Some examples of how to rearrange an equation to put it in transformation form are shown below.

Example 1

Write the following equation in transformational form: 25x² + 4y² = 100.

Solution:

Example 2

Write the following equation in transformational form:
9x² + 4y² + 18x - 32y + 37 = 0

Solution:

You should now be ready to do the work assigned for this lesson.

Activity

1. Complete Investigation 8 on pages 264 & 265 in your text.
2. Complete the Investigation Questions 42 - 47 on pages 265 & 266.
3. Do the CYU Questions 48 & 49 on page 266.

When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.

Test Yourself

Rewrite each of the following equations in transformational form. State the centre. Determine whether the graph is a circle or an ellipse. If it is a circle, state the radius. If it is an ellipse, state the length of the major an minor axes. Graph each equation.

1. 
2. 

[Solution]