Learning Resources

Home »  » Courses » Mathematics » Mathematics 3204 (delisted) » Unit 04 » Set 04 ILO 04 » Solution
Focus I: Using a Graphing Calculator to Explore Transformations of the Equation of a Circle

Test yourself

Answer the following questions about the circle with equation
x2 + y2 - 6x + 10y - 3 = 0.

  1. Rewriting the equation in standard form we get:
    x2 + y2 - 6x + 10y - 3 = 0
    x2 - 6x + y2  + 10y - 3 = 0
    (x2 - 6x + 9) + (y2  + 10y + 25) - 3 - 9 - 25 = 0
    (x - 3)2 + (y + 5)2 = 37
  2. The coordinates of the centre are ( 3 , -5) and the radius is .
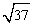  3. To rewrite the equation in a form suitable for graphing on the calculator we start with the standard form:
    (x - 3)2 + (y + 5)2 = 37
    (y + 5)2 = 37 - (x - 3)2 
    y + 5 = ±
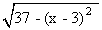
    y  = - 5 ±
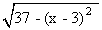
  4. A suitable "window" can be found by using the centre (3 , -5) and the radius of 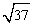, which is a little larger than 6. So set the x-values at 3 ± 7 and the y-values at -5 ± 7. This gives: Xmin = -4, Xmax =10, Ymin = -12, 
    Ymax = 2.

  5. Sketch the graph on your calculator.