Focus H: Interpreting Equations of Circles
Test yourself (Answers)
- Give the equation in general form of a circle with centre at (-4 ,
3) and radius 5.
Since we are given the centre and radius we can substitute directly
into the standard form for a circle. This gives: (x + 4)2
+ (y - 3)2 = 25. Now expand the binomials and rearrange
the terms to put it in general form.
(x + 4)2 + (y - 3)2 = 25
x2 + 8x + 16 + y2 - 6y + 9 =
25 (squaring
the binomials)
x2 + y2 + 8x - 6y + 16 + 9 -25 =
0 (rearranging)
x2 + y2 + 8x - 6y =
0
(the general form)
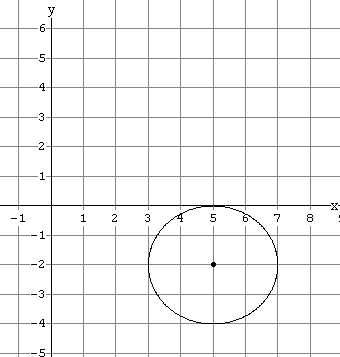
- Sketch the graph of 2x2 + 2y2 - 20x + 8y +
50 = 0.
First write the equation in standard form so that we can get the
coordinates of the centre and the radius:
2x2 + 2y2 - 20x + 8y +
50 = 0
x2 + y2 - 10x + 4y + 25 = 0
(dividing through by 2)
(x2 - 10x) + (y2 + 4y) + 25 =
0 (grouping like variables)
(x2 - 10x + 25) + (y2 +
4y + 4) + 25 - 25
- 4 = 0 (completing the square)
(x - 5)2 + (y + 2)2 = 4
(factoring)
Thus the coordinates of the centre are ( 5 , -2 ) and radius is 2
|

