
Learning Resources
Lesson
In the previous lesson we learned that the equation of circle with centre at the origin can be written as x2 + y2 = n, where n is the square of the radius. Thus the equation x2 + y2 = 50 is a circle with centre (0 , 0 ) and radius ![]() .
.
In previous work in this and other courses, you learned that in any equation with variables x and y, if x is replaced by x - h the graph is translated h units horizontally. Similarly, if y is replaced by y - k the graph is translated k units vertically.
If we combine the two ideas above, we should be able to write the equation of a circle whose centre is not at the origin. We would expect the graph of the equation ( x - h)2 + (y - k)2 = n to be a translation of the graph of x2 + y2 = n.
To test the above conjecture, do the investigation below. The equation of the graph we start with is x2 + y2 = 16. Note its centre and radius. Click on the arrows to see to where the graph will be translated when x and y are replaced by x - h and y - k. In your note book, write the equation and next to it record the coordinates of the centre and the radius for each graph. Do they agree with the conjecture we made above?
From the investigation on the previous page, it seems reasonable to conjecture that the equation of a circle with centre ( h , k) and radius r can be written as:
( x - h )2 + ( y - k )2 = r2
The above form of the equation is referred to as the standard form of the equation of a circle. We will learn about two other forms for the equation of a circle later in this unit, but for now we will concentrate on the standard form.
Some examples of how this form can be applied are given below.
Example 1
A circle whose equation is ( x - 5)2 + (y + 6)2 = 49 is translated 3 units to the left and 5 units up. Write the equation of the new circle. Write the mapping rule that maps the unit circle to the new circle.
Solution
First find the centre and radius of the original circle: centre (5 , -6) , radius = 7. Now translate the centre: 3 units left of 5 is 5 - 3 or 2; 5 units up from -6 is -6 + 5 or -1. The centre of the new circle is thus at (2 , -1) and the radius has not changed. To see this translation click the arrows below.
The equation of the new circle is: ( x - 2)2 + (y + 1)2 = 49
The rule to map the unit circle into this new circle is:
(x , y) ![]() (7x + 2, 7y - 1)
(7x + 2, 7y - 1)
Example 2
Graph the circle with equation: ( x + 3)2 + (y - 1)2 = 16
Solution
The centre of the circle is at (-3 , 1) and the radius is 4. Use this to draw graph with a set of compasses.
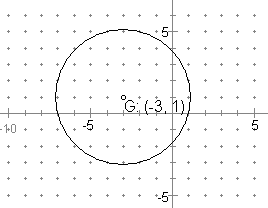
You should now be able to complete the work assigned for this lesson. Before you go to the top of the page and click the Activities button, read carefully the material in the margin on page 255 of your text. It summarizes a lot of what we have done with circles and you should copy it in your notebook for easy reference.
Activity
- Complete Investigation 7 on pages 254 & 255 in your text.
- Complete the Investigation Questions 7 - 11 on page 255.
- Do CYU Questions 12 - 20 on pages 255 - 257.
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
A circle has equation: ( x - 2)2 + (y + 3)2 = 25
- What are the coordinates of the centre and length of its radius?
- Draw its graph.
- Write the equation of the circle found by translating this circle 5 units to the left and 4 units up.