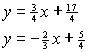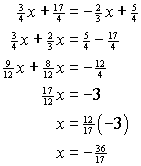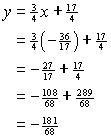Learning Resources

Focus G: Tangent Properties in a Coordinate System

Step F

This step requires you to find the intersection point of two lines for which you know the equations. One method of doing this is to read the coordinates of the point of intersection directly from the graph. This is the best method when the coordinates are integers. However, when the coordinates are not integers they are difficult, if not impossible, to read from the graph.

To find the coordinates of the point of intersection of any two line for which we know the equations we can solve the system of equations algebraically. An example of this is given below.

Example:

Find the point of intersection of the following two lines:   
                                        

Solution: 

Use the substitution method:
                                        

This means that the x-coordinate of the point of intersection of the two lines is . To find the y-coordinate of the point we must substitute this value into one of the original equations:
                                         

Thus the y-coordinate of the point of intersection is   and the point of intersection is

When you do this for the two lines in the Focus, the point of intersection should be  .

You may recall from other courses that a system of equations may be solved by several different methods. If you have done Math 2204, you might like to solve the above system using determinants and compare the results you obtain.