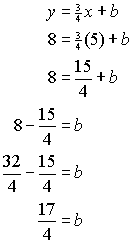Learning Resources

Focus G: Tangent Properties in a Coordinate System

Step C

The line perpendicular to the radius will have a slope that is the negative reciprocal of the slope of radius.  For example: if the slope of the radius is then the slope of the line perpendicular is  ; if the slope of the radius is then the slope of the perpendicular is .

To find the equation of a line you will have to recall your work from a previous course. One form of a linear equation is given in the margin on page 248 of your text. The equation of any non-vertical straight line can also be written in the following form (called the slope and y-intercept form):

where m is the slope and b is the y-intercept.

In this problem you have the slope of the perpendicular and the coordinates of a point it passes through. You do not have the y-intercept. So how do you find the equation. Look at the example below and use it as a model to find the equation of the perpendicular.

Example

Find the equation of the line through (5, 8) with slope 3/4.

Solution

You know the value of m, the slope, so substitute that into the equation:

To determine the value of b, substitute in the coordinates of the point (5 , 8) and solve for b:

So the equation is