Learning Resources
Lesson
We have already defined the term tangent to a circle. It is a line that touches a circle at only one point. In this lesson we will investigate some of the properties of tangent lines.
You have two methods of exploring the properties presented in this Investigation. One is to use the method described in your text on page 243. The other is to use the Geometer's Sketch Pad interactions provided below.
Text Method
This method involves paper folding and the steps are described on page 243 in your text. To do it you will need some paper, a set of compasses, and a ruler. Be sure to record in your notebook the answer to Step E and Step H. These are properties that you will use in other proofs and calculations. Also, be sure to record in your notebook the answer to Investigation Question 47(f) as this is also an important property that you will use in the future. If you have any difficulty with this method of doing the investigation, you can click here for some help and hints.
Geometer's Sketch Pad Method
Once you have started to do the investigation, the diagram may get messed up. If it does, to return to the original screen you started with, simply press r. This will restore the screen to the original diagram. When you are finished with the investigation, simply close the window and you will be returned to this page.
The first interactive window replaces Steps A to E in your text and deals with making a conjecture about the angle formed by a tangent and a radius drawn to the point of tangency. Be sure to record in your notebook the answer to Step E before you go on to the next part of the investigation. You should round the measures of the angles you are investigating to the nearest degree. Click here to start investigating the relation between a tangent and a radius (diameter) drawn to the point of tangency.
The second interactive window replaces Steps F to H in your text and deals with the distance from a point of intersection of two tangents to their respective points of tangency on the circle. Be sure to record in your notebook the answer to Step H before you go on to the next part of the investigation. Click here to start investigating the relation now.
The third interactive window replaces Investigation Question 47(a) - (e) on page 244 in your text and deals with the relation of a tangent chord angle to an inscribed angle intercepting the same arc. Be sure to record in your notebook the answer to 47(f) on page 244 before you go on to the next part of the this lesson. Click here to start investigating the relation now.
If you are sure you understand the properties that were presented in the investigation, you may go to the top of the page and click the activities button to proceed with the work on this lesson.
1. The angle formed by a tangent line and a radius drawn to the point of tangency is a right angle:
Ð ACE = 90°, Ð ACD = 90°, and AC ^ DE
2. The point of intersection of two tangents to the same circle is equidistant from their respective points of tangency: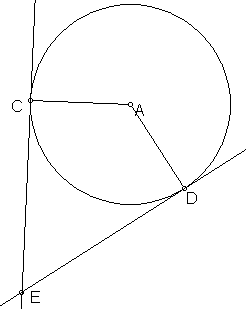
EC = ED
3. The angle between a tangent and a chord is equal to the inscribed angle on the opposite side of the chord (i.e. intercepting the same arc):
mÐ KHM = mÐ HJM (Hint: Note the arc in blue, it lies in the interior of both the tangent chord angle and the inscribed angle.)
Activity
- Answer in your notebook the questions in Steps E and H of Investigation 5 on pages 243 & 244 in your text.
- Answer in your notebook the question in the Investigation Question 47(f) on page 244.
- Do the CYU Questions 48 - 51(a) on pages 244 & 245.
When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.
Test Yourself
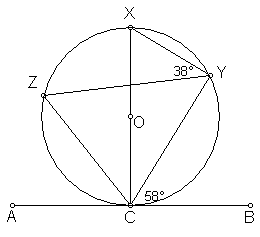
1. In the diagram below, AB is a tangent at C and XC is a diameter.
mÐ YCB = 58° and mÐ XYZ = 38°.
Find the following:
mÐ YXC, mÐ YZC, mÐ YCX, mÐ ZCA, mÐ ZCX, mÐ ZYC,