Learning Resources

Lesson

In addition to your note book, you will need the following to work with the concepts and problems in this section:

• a ruler
• a set of compasses
• a protractor

In this lesson you will be dealing with several new terms so the first thing we will do is look at a definition for those terms and see them in a diagram.

You are probably already familiar with the term arc. It is nothing more than a segment or piece of a curve. In our case the curve is a circle. If the arc is half the circle, it is called a semi-circle. The diagram below shows two semi-circles, the red arc and the blue arc..

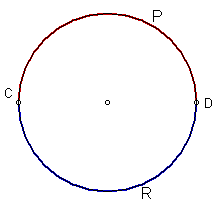
To name a semi-circle requires three letters. This is necessary in order to avoid confusion about which arc is being referred to. For example in the above diagram, if we simply use we do not know if we are referring to the red or blue arc. To refer to the red arc we would use the notation and for the blue arc we would use

The diagrams below show two different arcs which are not semi-circles. The red one on the left is called a minor arc, the blue one on the right is called a major arc. It should be fairly obvious that minor refers to arcs less than a semi-circle and major refers to arcs that are greater than a semi-circle.

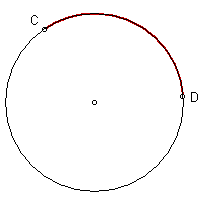
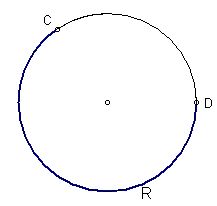
Minor arcs can be named using just two letters. In the diagrams above, if we write it automatically assumes we mean the minor arc. That is the convention that is used in all mathematics texts. If we wish to refer to the major arc, we must put a point on it and use three letters. Thus in the diagrams above we have no way of naming the major arc in the one on the left. In the diagram on the right we can write for the major arc.

We now need to turn our attention to how to measure these arcs.

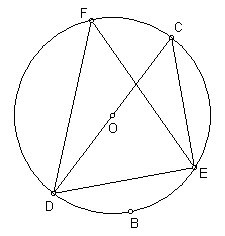
Associated with every arc there is a central angle. A central angle is an angle with vertex at the centre. If the sides of the angle pass through the end points of the arc, we say the central angle intercepts the arc and the arc subtends the angle. This is illustrated in the diagram below.

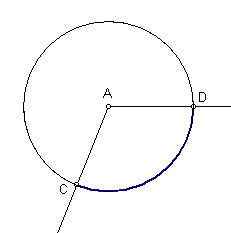
In the diagram above ÐCAD is a central angle and its sides contain points C and D, the endpoints of the . We therefore say that subtends ÐCAD and ÐCAD intercepts . Notice that the arc is in the interior of the angle.

By definition, the measure of an arc is equal to the measure of its central angle. The measure of an arc is thus given in degrees. In the above diagram we would use the following notation to write the measure of the arc:
m= mÐCAD

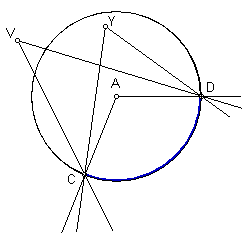
Any angle can intercept an arc, but only the central angle has measure equal to the arc. Consider the diagram below. All three angles, ÐCVD, ÐCYD, and ÐCAD intercept the arc, but only ÐCAD has measure equal to the arc.

It is also important to note that an arc is measured in degrees and not in centimeters or some other unit of length. The measure of an arc and the length of an arc are two totally different things and this is indicated in the diagram below.

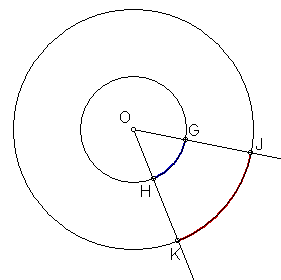
In the above diagram because they both subtend the same central angle at O. However, it is fairly obvious that the distance from H to G measured along the arc is not the same as the distance from K to J measured along the arc. Arc length depends on both the central angle AND the length of the radius. In this lesson we are only interested in the measure of the arc not its length.

We have to consider one more special angle before we begin our investigation.

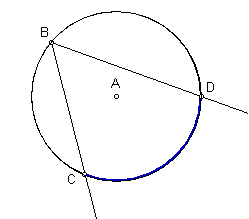
The angle we wish to investigate is called an inscribed angle. By definition, it is an angle whose vertex lies on a circle and whose arms contain arcs of a circle. It is shown in the diagram below. We say ÐCBD is an inscribed angle which intercepts . We can also say that subtends ÐCBD.

We now wish to investigate some of the relationships that exist between all the various angles and arcs we have just been discussing. There are two ways for you to proceed. One is to use the method described in your text, the other is to use Geometer's Sketch Pad in the interactive window provided below.

Text Method

Simply follow the directions in your text for Steps C to K. The main thing to record and mark plainly in your note book is the answer to Steps G, J, and K.

Geometer's Sketch Pad Method (replacing steps C to F)

For the first part of the investigation, open the window and click on point A. Drag A to several locations and record the measure of the central and the inscribed angle. After you have made these observations, use them to answer Step G of the Investigation on page 234 in your text. Record you answer in your note book.

Once you have started to investigate the different positions for A, the diagram may get messed up. If it does, to return to the original screen you started with, simply press r. This will restore the screen to the original diagram. When you are finished with the investigation, simply close the window and you will be returned to this page.

Geometer's Sketch Pad Method (replacing steps H and I)

The next part of the investigation is to discover a relation between two inscribed angles that intercept the same arc. Again open the window and drag A or B to several locations and record the measure of the two angles. After you have made these observations, use them to answer Step J of the Investigation on page 234 in your text. Record your answer in your note book.

Geometer's Sketch Pad Method (replacing step K)

The final part of the investigation is to discover a relation about an inscribed angle which intercepts a semi-circle. After you have made your observations, use them to answer Step K of the Investigation on page 234 in your text. Record your answer in your note book.

After you have finished your investigations, either by using the text method or the GSP method, continue reading below for a summary.

1. A minor arc is an arc with a measure less than 180° and a major arc is an arc with a measure greater than 180°.
2. An arc with a measure of 180° is a semi-circle.
3. The measure of an arc is equal to the measure of the central angle it subtends.
4. An inscribed angle is half the measure of the arc it intercepts and therefore half a central angle intercepting the same arc.
5. Inscribed angles intercepting the same arc have equal measures.
6. An angle inscribed in a semi-circle is a right angle.

You should print off the above definitions and put them in your notebook or binder for future reference.

You should now be able to the the exercises in the text associated with this lesson.

Activity

1. If you have not already done so, record in your notebook the answer to Steps G, J and K of Investigation 4 on pages 232 - 234 in your text.
2. Complete the Investigation Questions 1 - 11 on pages 234 - 236.
3. Do the CYU Questions 12 - 15 on pages 236 & 237.

When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.

Test Yourself

1. Given: In the diagram below m = 96° and DF = EF. Find: mÐ CDF, m Ð CEF, and mÐ CDE

[Solution]