Learning Resources

Lesson

If we are given two points A(x₁ , y₁) and B(x₂, y₂), we have a formula that allows us to calculate the slope of the line or segment that contains them. We have worked with this formula in the previous lesson on parallel and perpendicular lines.

The question now is this: if we are given two points, A(x₁ , y₁) and B(x₂, y₂), can we develop a formula that will give us the distance between them? Alternately we could say we are looking for a formula for the length of the segment that has these end points. To see the development of this formula, commonly referred to as the distance formula, click here.

A second question related to the points A(x₁ , y₁) and B(x₂, y₂) is whether we can find a formula that will give us the coordinates of the midpoint of the segment.

Once you have seen where the formulas come from, the next step is to apply them to solving problems.

Example 1

Given the quadrilateral CDEF with vertices C(-10 , 3), D(-7 , 11), E(1 , 14), and F(-2 , 6). Show that CDEF is a rhombus and that its diagonals bisect each other (i.e., have the same midpoint).

Solution

The first thing with any problem involving coordinates is to plot the points on a grid:

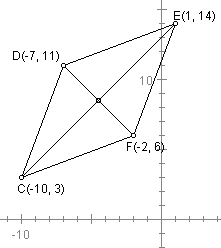
By definition, a rhombus is a quadrilateral with four equal sides. Use the distance formula to calculate the length of each side:

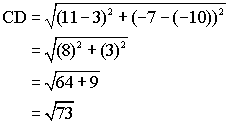
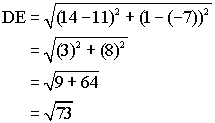
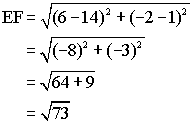
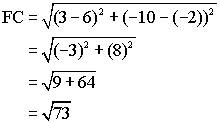
Since all four sides have length they are equal and the quadrilateral is a rhombus.

Now check the midpoints of the diagonals. If the diagonals have the same mid-point, then they bisect each other.

Mid-point of CE Mid-point of DF

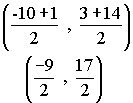
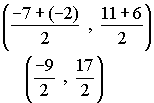
Thus CE and DF bisect each other.

Summary

Given points P(x₁ , y₁) and Q(x₂ , y₂), then:

The length of PQ, or the distance formula , is:

The mid-point of PQ is:

Activity

1. Read through the examples in Focus C on pages 224 - 226 in your text.
2. Complete the Focus Questions 10 -15 on page 226 & 227.
3. Do the CYU Questions 16 - 21, 23, 26, 27 on pages 227 - 229.

When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.

Test Yourself

Given a triangle with vertices J(-5 ,-8), K(9 , 8), L(1 , 15):

1. Is the triangle a right triangle?
2. What are the coordinates of the mid-point of its longest side?
3. What is the distance from the mid-point of its longest side to the three vertices? What do you notice about the distances?

[Solutions]